传感器与检测技术

70%开卷考试+30%乐学提交作业

慕课非强制，9~13 章节与本课程无关

课程内容包括传感器工作原理、基本结构、性能特点、应用方法、传感器技术发展；检测技术基本概念和数据处理方法。

第一章 传感器概述与特性

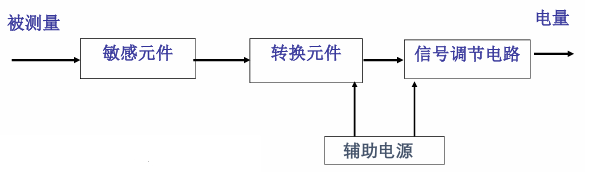
传感器在 GB7665-87 中定义为，能感受规定的被测量并按照一定规律转换成可用输出信号的器件或装置，处于研究对象与测控系统的接口位置。

传感器的组成结构如图

传感器分类有多种方式：

• 按输入量分类：位移、速度、温度、压力等

  常见的被测物理量有机械量(长度、厚度、位移、速度、加速度、旋转角、转速、质量、重量、力、压力、真空度、力矩、风速、流速、流量)，声学量(声压、噪声)，磁学量(磁通、磁场)，热学量(温度、热量、比热)，光学量(亮度、色彩)

• 按工作原理分类：应变式、电容式、电感式、压电式、热电式

• 按物理现象分类：结构型传感器(依靠传感器结构参数的变化实现信号转变)、物性型传感器(依靠敏感元件材料本身物理性质的变化实现信号变换)

• 按能量关系分类：能量转换型传感器、能量控制型传感器

  能量转换型传感器直接由被测对象输入能量使其工作(如热电偶温度计、压电式加速度计)，能量控制型传感器从外部供给能量并由被测量来控制外部供给能量的变化(如电阻应变片)

• 按输出信号分类：模拟式传感器、数字式传感器

1.1 静态特性

线性度

静态特性用多项式方程\(y = a_{0} + a_{1} x + a_{2} x^2 + \cdots + a_{n} x^n\)来表示，\(a_{0}\)称为零点输出，\(a_{1}\)称为理论灵敏度/线性灵敏度，其它项系数均为非线性系数。理想的传感器是线性的，输出和输入之间有严格的比例关系，因此会使用直线对实际的特性曲线进行拟合，线性度就是实际特性和拟合特性的差异，定义为：

\[\gamma_\text{L} = \pm \frac{\Delta L_\text{max}}{y_\text{FS}}\times 100 \%，其中y_\text{FS}为满量程，是传感器实际输出的最大值减去最小值\]

实际特性由校准/标定的方式获得，即采集标准输入(环境标准，设备标准)下的输出并列出数据表格；由小到大的正行程和由大到小的反行程分别进行平均，两个平均后的结果再进行平均，得到实际特性。

获得拟合直线的方式有多种，常用的拟合方式有：理论拟合、过零旋转拟合、端接拟合、端接平移拟合、最小二乘拟合(残差平方和\(SSE\)最小)

注意：以上的拟合方式，均仅适用于传感器的非线性不明显的情况，如果传感器特性呈现明显非线性，则可以使用分段拟合、软件打表等方式进行拟合

迟滞

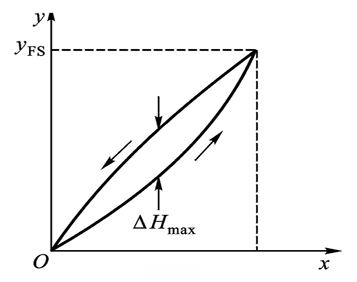
正行程和反行程输入-输出曲线不重合，即输入的方向不同导致输出特性也不同的现象，属于系统误差。传感器机械结构的磨损、数据延迟等都可能导致迟滞现象

\[\gamma_\text{H} = \pm \frac{1}{2}\frac{\Delta H_\text{max}}{y_\text{FS}}\times 100\%\]

重复性

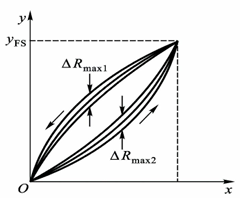
传感器输入按同一方向作全量程连续多次变动时所得特性曲线不一致的程度，属于偶然误差。偶然误差越小，复现性越强。重复性可以针对单个测点或针对全量程进行评价。

单个测点重复性的定义基于标准差，标准差可以表征数据的分散程度：

\[\begin{aligned} &\xi_\text{R} = \frac{\sigma\cdot a}{y_\text{FS}}，\sigma为标准差，a为置信概率\\ &\sigma = \sqrt{\frac{\sum_\text{i=1}^n(x_\text{i} - \overline{x})^2}{n - 1}} \quad (注意是有限次测量，分母为n-1)\\ \end{aligned}\]

全量程下的重复性定义为正反行程所有测点中最大误差与满量程的比值

\[\gamma_\text{R} = \pm \frac{\Delta R_\text{max}}{y_\text{FS}}\times 100\%\]

灵敏度与灵敏度误差

灵敏度定义为输出的变化量与引起该变化量的输入变化量之比，实质上就是输出——输入特性曲线上各个点的斜线斜率，表征了传感器对微小变化的敏感程度

\[k = \frac{\Delta y}{\Delta x}\]

显然，线性传感器的灵敏度为常数，非线性传感器的灵敏度为变量，传感器要在灵敏度较高的范围内使用。灵敏度受到温度的影响，因此也存在灵敏度误差，定义为

\[\gamma_\text{s} = \frac{\Delta k}{k}\times 100\%\]

分辨率和阈值

事实上，传感器的实际输出曲线是离散的阶梯状，阶梯对应的输入量的范围就是分辨能力，只有超过这个范围，输出量才会发生改变。分辨率就是传感器能检测到的最小输入增量，阈值是指在输入零点附近的分辨率。

灵敏度是传感器输入——输出特性曲线的斜率，是较为宏观的指标；而分辨率是描述这种阶梯状曲线中阶梯宽度的，是较为微观的指标

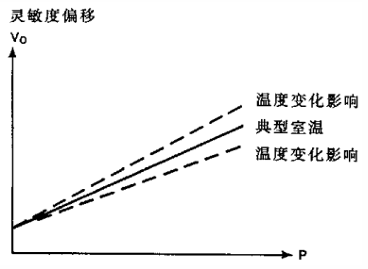
稳定性和温度稳定性

稳定性即传感器在长时间工作情况下输出量发生的变化，有时也用标定周期/校准周期来表示，在标定周期内可以保证传感器性能。材料和元器件是影响稳定性的两个主要因素。温度稳定性即传感器在外界温度变化情况下输出量发生变化的现象，用温度误差系数\(\alpha\)定量描述这一指标，即温度发生 1℃ 变化时输出的改变量。

静态误差

综合以上单项误差指标得到静态误差(主要综合前面四项)，指的是传感器在全量程内任一点的输出值与理论输出值的偏离程度。

综合的方法有：

• 均方误差(即假设各项误差互不影响)：线性度和迟滞属于系统误差、重复性属于偶然误差，理论上讲两者不能简单地直接叠加

  \[\delta = \pm \sqrt{\gamma_\text{L}^2 + \gamma_\text{H}^2 + \gamma_\text{R}^2 + \gamma_\text{S}^2}\]

• 求标准差(将拟合直线与实际曲线在各测点的误差看作随机分布)：用标准差表示 \(\sigma = \sqrt{\frac{1}{n-1}\sum_\text{i=1}^n(\Delta y_{i})^2}\)

1.2 动态特性

传感器动态特性地数学模型由微分方程或传递函数描述，分析方式和性能指标与自控原理中的完全一致，如固有频率就是一种动态特性

常见传感器的数学模型只有三种，即零阶环节、一阶环节和二阶环节。零阶环节是理想的传感器，输出与输入有严格地比例关系且无延迟；一阶环节的关键参数为时间常数\(\tau\)，决定了传感器的响应速度；二阶环节的关键参数为无阻尼固有频率\(\omega_\text{n}\)和阻尼比\(\xi\)(阻尼固有频率\(\omega_\text{d} = \sqrt{1-2\xi^2}\omega_\text{n}\))。

时域性能指标包括时间常数\(\tau\)、上升时间\(t_\text{r}\)、响应时间\(t_\text{s}\)、超调量\(M\%\)。频域性能指标包括幅频特性\(A(\omega)\)和相频特性\(\phi(\omega)\)：阻尼比小于 1 时，在\(\omega\)接近\(\omega_\text{n}\)时存在谐振峰，实践表明当\(\xi \geqslant 0.707\)时可以基本抑制谐振；另外，在频率特性曲线中的平坦区域使用传感器才能保证其灵敏度为常数。

设计传感器应该设计在欠阻尼状态，较快响应且具有较宽的线性工作范围。一般来说，\(\xi\)取 0.6~0.8 可以兼顾系统的稳定性和响应灵敏度，认为\(\xi=0.707\)为最佳阻尼比。\(\omega_\text{n}\)由传感器内部构造决定，\(\omega_\text{n}\)越高，系统达到稳定状态的速度越快，传感器的工作频率也越高，工作频带也就越宽。传感器的信号频率/工作频率\(\omega\)应低于系统固有频率\(\omega_\text{n}\)的 3-5 倍，以使系统对检测信息的变换保持良好的线性特征(工作频率远离输入频率)。

第二章 电阻式传感器

电阻式传感器有电位器式(测量位移)和应变片式(测量力)两种。

2.1 电位器式传感器

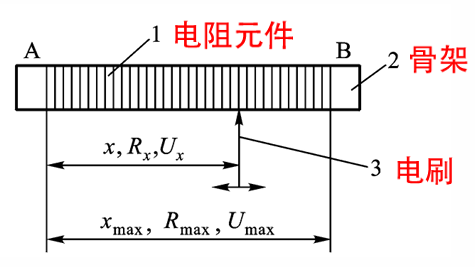
电位器有绕线式和旋转式两种，前者测量线位移后者测量角位移，两者原理和功能完全相同，下面以绕线式为例进行分析

按行程和电阻的关系也可分为线性电位器和非线性电位器两种。线性传感器对组成结构的要求包括：骨架截面处处相等、电阻丝绕线节距(每匝线圈之间的间距)处处相等、金属丝的电阻率和横截面积处处相等。使用非线性电位器的原因有二：一是为了刻意制造某种函数，如指数函数、对数函数等；二是为了补偿仪器仪表本身的非线性特征，使得整体的输出呈线性特征。

基本特性

显然，电位器式传感器需要接在相应的测量电路中使用，测量电路对传感器有输入阻抗的影响。当输入阻抗为无穷大时，传感器特性称为空载特性，是理想传感器的输入输出特性：

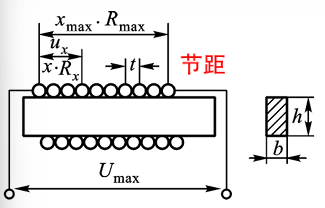
\[R_{x} = \frac{x}{x_\text{max}}R_\text{max} \quad U_{x} = \frac{x}{x_\text{max}}U_\text{max}\]

线性电位器的灵敏度：

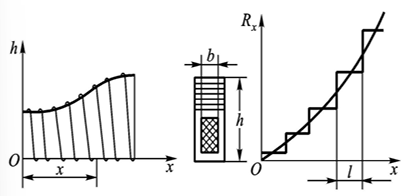
\[\begin{aligned} &k_\text{R} = \frac{2(b+h)\rho}{At} \quad (电阻灵敏度) \\ &k_\text{U} = \frac{2(b+h)\rho}{At} I \quad (电压灵敏度) \\ &A为金属丝截面积，t为节距 \end{aligned}\]

非线性电位器的灵敏度：

\[k_\text{u} = \frac{\text{d}U_{x}}{\text{d}x} = \frac{2(b+h)\rho}{At}I \quad (电压灵敏度)\]

可改变节距\(t\)或设计成变骨架式电位器\(h = \frac{At}{2\rho I}\left( \frac{\text{d}U_{x}}{\text{d}x} \right) -b\)

阶梯特性

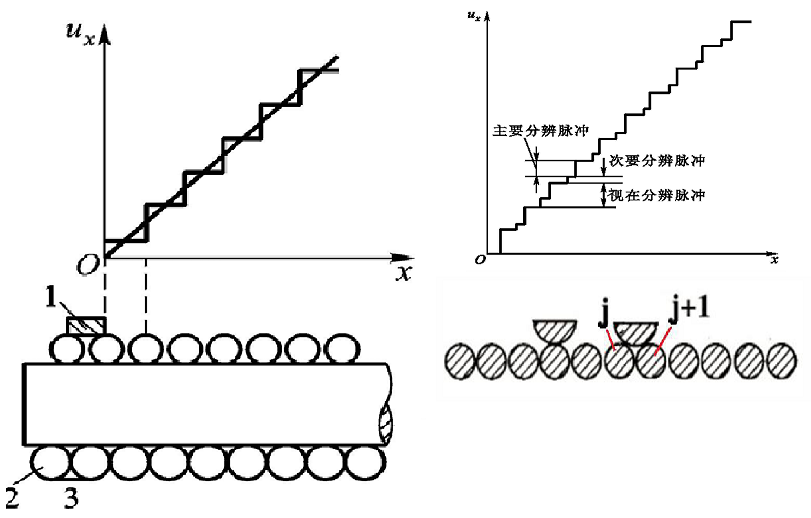
即使是线性电位器，从微观结构的角度分析，由于线圈是一匝一匝缠绕的，因此存在阶梯特性

在理想阶跃特性曲线中，这种阶跃值称为视在分辨脉冲\(\Delta U = \frac{U_\text{max}}{N}\)，\(N\)为匝数。在实际的阶梯特性中，由于电枢短接两匝线圈会使得匝数减一，故实际的阶跃还有次要分辨脉冲

\[\Delta U_\text{n} = \frac{U_\text{max}}{n-1}j - \frac{U_\text{max}}{n}j = U_\text{max}\left( \frac{1}{n-1} - \frac{1}{n} \right)j\]

评价这种阶梯特性的指标如下：

\[\begin{aligned} &阶梯误差：:r_{j} = \pm \frac{\frac{1}{2}\cdot\frac{U_\text{max}}{N}}{U_\text{max}} = \pm\frac{1}{2N}\\ &行程分辨率:e_\text{by} = \frac{\frac{x_\text{max}}{N}}{x_\text{max}} \times 100\% = \frac{1}{N} \times 100 \%\\ &电压分辨率:e_\text{ba} = \frac{\frac{U_\text{max}}{N}}{U_\text{max}} \times 100\% = \frac{1}{N} \times 100 \%\\ \end{aligned}\]

除了电位器本身结构造成的误差外，制造时的工艺误差也可能带来非线性特征，如：电阻丝的电阻率和直径不均匀、骨架偏离规定的几何尺寸、节距不均匀、电刷接触点的抛光误差等。

负载特性

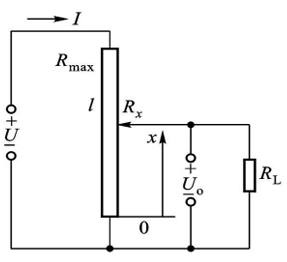
当不能忽略测量电路输入阻抗带来的影响时，需要分析负载特性

显然，根据\(R_{x}\)与\(R_\text{L}\)并联再与\(R_\text{max}-R_{x}\)串联的分压关系：

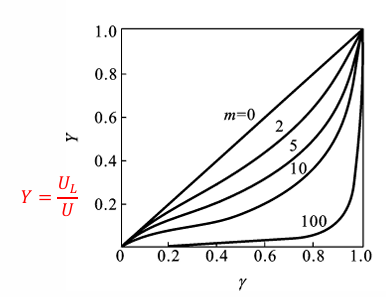
\[\begin{aligned} U_\text{o} &= \frac{\frac{R_{x}R_\text{L}}{R_{x} + R_\text{L}}}{\frac{R_{x}R_\text{L}}{R_{x} + R_\text{L}}+R_\text{max}-R_{x}}U\\ &= \frac{R_{x}R_\text{L}}{R_\text{L}R_\text{max}+R_{x}R_\text{max} - R_{x}^2}U\\ &=\frac{r}{1+rm(1-r)}U\\ 其中r &= \frac{R_{x}}{R_\text{max}}(电阻相对变化)\\ m&=\frac{R_\text{max}}{R_\text{L}}(负载系数) \end{aligned}\]

由此可作出电位器的负载特性曲线族，当\(m=0\)时，为空载特性曲线，\(U_\text{L}\)与\(U\)成线性关系

负载输出\(U_\text{L} = \frac{r}{1+rm(1-r)}U_\text{max}\)，空载输出\(U_{0} = rU_\text{max}\)，将二者进行比较得到负载误差

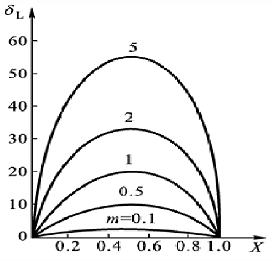
\[\begin{aligned} \delta_\text{L} &= U_{0} - U_\text{L} \quad (绝对量)\\ \delta_\text{L} &= \frac{U_{0} - U_\text{L}}{U_{0}} = 1-\frac{U_\text{L}}{U_{0}} = 1-\frac{1}{1+rm(r-1)} \end{aligned}\]

由此可作出电位器的负载误差曲线，显然\(r=0.5\)时误差达到极大值，\(\delta_\text{L} = 1-\frac{1}{1+\frac{1}{4}m}\)，根据此式从要求的负载误差范围得出测量电路负载和电位器电阻值的关系，例如要求\(\delta_\text{L} < 0.01\)，则\(R_\text{L} > 25R_\text{max}\)

特点

电位器设计的目标是噪音小、非线性小、分辨率高、稳定性好，对各个组成部分有对应的要求

• 电阻丝：电阻率高，电阻温度系数小，耐腐蚀，耐磨、与铜接触电势小。选用康铜(温度系数小)、镍铬(电阻率大)、镍铬铁合金(卡玛丝，温度系数小且电阻率大，但接触电阻大，需要电刷压在电阻丝上)、铂铱合金(化学稳定性好)等材料
• 电刷：抗氧化，接触电势小，噪声低，与电阻丝硬度相近或偏高，具有一定接触压力。选用银、铂铱合金、铂铑合金等材料
• 骨架：膨胀系数与金属丝相近(避免影响应变特性)，绝缘性好，形状稳定，散热好。选用陶瓷、酚醛树脂、工程塑料等材料

电位器式传感器的特性有

• 结构简单、成本低
• 稳定性好、线性度高
• 输出信号大
• 准确度高(0.05%)
• 只能在低频工作(电刷滑动)
• 要求输入能量大
• 寿命短(电刷摩擦)
• 电噪声大

电位器配合齿轮齿条可侧线位移角位移，配合弹性敏感元件可测压力，配合惯性质量块、弹簧和阻尼器构成的三自由度二阶系统可测加速度速度位移。

2.2 应变片式传感器

应变片式传感器的敏感元件是金属箔片，也称为敏感栅。应变片配合弹性敏感元件可以测量位移和扭矩等。

应变效应

电阻两端受力导致阻值发生变化的现象称为应变效应

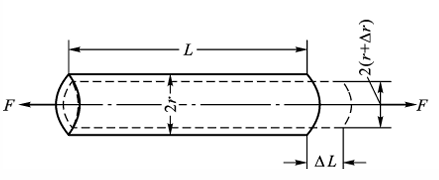
\[\begin{aligned} R &= \frac{\rho l}{S}\\ \text{d}R &= \frac{\rho}{S}\text{d}l + \frac{l}{S}\text{d}\rho - \frac{\rho l}{s}\text{d}S\\ \frac{\text{d}R}{R} &= \frac{\text{d}\rho}{\rho} + \frac{\text{d}l}{l} - \frac{\text{d}S}{S}\\ \frac{\Delta R}{R} &= \frac{\Delta l}{l} + \frac{\Delta \rho}{\rho} - \frac{\Delta S}{S}\\ &= \frac{\Delta l}{l} + \frac{\Delta \rho}{\rho} - 2\frac{\Delta r}{r} \end{aligned}\]

材料力学知识补充：(注意这里的\(\mu\)往往是试件的)

\[\begin{aligned} \varepsilon &= \frac{\Delta l}{l} \quad (轴向应变/横向应变)\\ \varepsilon_\text{r} &= \frac{\Delta r}{r} \quad (径向应变)\\ 在弹性范围内: \varepsilon_\text{r} &= -\mu \varepsilon,其中\mu为材料应变系数/泊松系数\\ \frac{\Delta \rho}{\rho} &= \pi_\text{e} E \varepsilon,其中\pi_\text{e}为压阻系数,E为弹性模量\\ \varepsilon &= \frac{\sigma}{E} = \frac{F}{SE}，其中\sigma为应力，相当于物理中的压强 \end{aligned}\]

将应变现象式子简化如下，其中第一项描述了形变效应，第二项描述了压阻效应。金属材料以形变效应为主，半导体材料以压阻效应为主，在工程上可忽略次要影响因素。(注意这里的\(\mu\)是应变片的)

\[\frac{\Delta R}{R} = (1+2\mu)\varepsilon + \pi_\text{e} E \varepsilon = (1 + 2\mu + \pi_\text{e} E)\varepsilon\]

定义灵敏系数如下，描述了单位形变所引起的电阻相对变化：

\[K = \frac{\Delta R}{\varepsilon R} = 1 + 2\mu + \pi_\text{e} E\]

金属材料的\(K\)在 1.7-3.6，半导体材料的\(K\)在 100 左右，但半导体材料的阻值和灵敏系数受温度影响较大，金属材料这两个参数的温度稳定性好。本课程以金属材料为例讨论，忽略压阻效应。

结构材料

应变片式传感器的结构由敏感栅、基底(绝缘，粘贴)和盖层(防潮防尘)构成，敏感栅中，与主应力方向一致的称为纵栅，与主应力方向垂直的称为横栅。敏感栅有丝式和箔片式，丝式由金属丝反复缠绕而成(R 大且接触点小)。

箔片式由光化学腐蚀或精密冲压形成，可获得较为复杂的敏感栅图案(可有多个敏感栅轴向)，适用于主应力方向未知的情况。箔片式由于横栅面积大，产生的横向效应小(横向效应是指，应变片受力时，垂直于受力方向会产生与主应力方向相反的应变，从而产生削弱电阻变化，使得灵敏度降低的现象)。此外，箔片式的外形薄，利于应变传递；材质柔软可用于曲面应力测量

对敏感栅材料的要求

• 灵敏系数大，在较大应变范围恒定
• 电阻率高(\(\Delta R = K \varepsilon R\)，电阻大灵敏度高)
• 电阻温度系数小(\(\Delta R_\text{t}\)小，受温度影响小)
• 机械强度高，易于拉丝与辗薄
• 与其它金属的接触电势小

常用材料有：康铜、镍铬合金、镍铬铁合金、贵金属

主要特性

• 灵敏系数(应变片的灵敏系数受结构影响，会略小于应变片的灵敏系数，一般由实验测定)\(K = \frac{\frac{\Delta R}{R}}{\varepsilon} < K_{0}\)

• 横向效应：\(\Delta R = \Delta R_{x} - \Delta R_{y}\)

• 温度效应：电阻的变化来自应变和温度变化两部分，由温度变化引起的又细分为两部分，一是由电阻温度系数引起的，二是由应变片和试件膨胀系数不同造成附加形变引起的

  \[\begin{aligned} &\frac{\Delta R}{R} = \left(\frac{\Delta R}{R}\right)_\varepsilon + \left(\frac{\Delta R}{R}\right)_{t}\\ &\Delta l_\text{s} = \beta_\text{s} \Delta t l \quad \Delta l_\text{g} = \beta_\text{g} \Delta t l\\ &\varepsilon' = \frac{\Delta l}{l} = (\beta_\text{g} - \beta_\text{s})\Delta t\\ &\left(\frac{\Delta R}{R}\right)_{t_{2}} = K\varepsilon' = K(\beta_\text{g} - \beta_\text{s})\Delta t \\ &\left(\frac{\Delta R}{R}\right)_{t} = \left(\frac{\Delta R}{R}\right)_{t_{1}} + \left(\frac{\Delta R}{R}\right)_{t_{2}} = \alpha_{t} \Delta t + K(\beta_\text{g} - \beta_\text{s})\Delta t\\ &\varepsilon_{t} = \frac{\left(\frac{\Delta R}{R}\right)_{t}}{K} = \frac{\alpha_{t} \Delta t}{K} + (\beta_\text{g} - \beta_\text{s})\Delta t \quad (虚假应变)\\ &e_{t} = \frac{\varepsilon_{t}}{\varepsilon} \times 100 \% \quad (温度误差) \end{aligned}\]
• 迟滞、零飘(无输入时使出波动)、蠕变(输入不变时输出波动)
• 疲劳寿命(焊接影响疲劳寿命)、绝缘电阻、动态响应

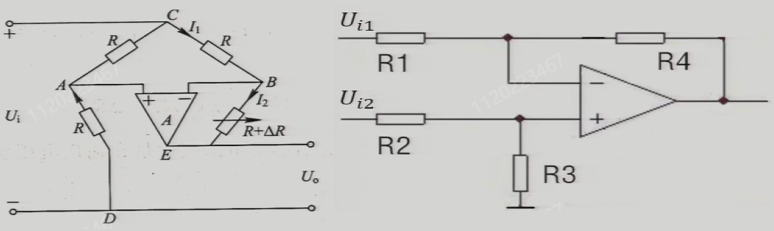
直流电桥

直流电桥的平衡条件为：相对桥臂之积相等 / 相邻桥臂电阻比值相等(可以假设输入电压负极处为零电位，根据串联分压原理计算出输出电压两端点位，从而得到电位差)

\[\begin{aligned} &U_\text{o}=\frac{R_{1}}{R_{1} + R_{2}}U-\frac{R_{3}}{R_{3} + R_{4}}U=\frac{R_{1}R_{4}-R_{2}R_{3}}{(R_{1}+R_{2})(R_{3}+R_{4})}U\\ &故R_{1}R_{4}=R_{2}R_{3} \quad 或 \quad \frac{R_{1}}{R_{2}}=\frac{R_{3}}{R_{4}} \end{aligned}\]

定义桥臂比\(n = \frac{R_{2}}{R_{1}}\)，单臂电桥的电压灵敏度(\(R_{1}\)变化为\(R_{1} + \Delta R_{1}\)代入式子)：

\[\begin{aligned} 输出电压:U_\text{o}&=\frac{(R_{1}+\Delta R_{1})R_{4}-R_{2}R_{3}}{(R_{1}+\Delta R_{1}+R_{2})(R_{3}+R_{4})}U\\ &= \frac{\frac{R_{4}}{R_{3}}\frac{\Delta R_{1}}{R_{1}}}{(1 + \frac{R_{2}}{R_{1}}+\frac{\Delta R_{1}}{R_{1}})(1+\frac{R_{4}}{R_{3}})}U\\ &\approx\frac{n}{(1 + n)^{2}}\frac{\Delta R_{1}}{R_{1}}U\\ 电压灵敏度:K_\text{u}&=\frac{U_{0}}{\frac{\Delta R_{1}}{R_{1}}}=\frac{n}{(1 + n)^{2}}U \end{aligned}\]

由上式看出，当\(n=1\)时(此时称为等臂电桥)，灵敏度取得极大值\(K = \frac{1}{4}U\)；想要提高灵敏度可以适当升高电压，但要注意电压升高电流增大发热造成的温升

上式的约等于处引入了非线性误差：

\[\begin{aligned} &理想输出 \quad U_\text{o}'=\frac{1}{4}\frac{\Delta R_{1}}{R_{1}}U\\ &实际输出 \quad U_\text{o}=\frac{\frac{\Delta R_{1}}{R_{1}}}{4(1+\frac{1}{2}\frac{\Delta R_{1}}{R_{1}})}U\\ &非线性误差 \quad \delta=\frac{U_\text{o}-U_\text{o}'}{U_\text{o}'}=-\frac{1}{2}\frac{\Delta R_{1}}{R_{1}} \end{aligned}\]

使用恒流源供电的电桥可以改善非线性误差：(实际输出中，分母系数由\(\frac{1}{2}\)变为\(\frac{1}{4}\))

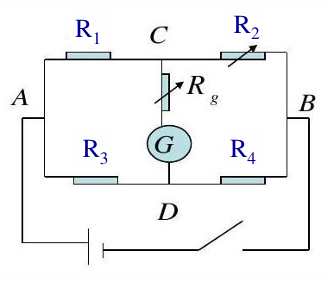
上述模式被称为工作在小偏差不平衡电桥的工作模式，与不平衡电桥相对应的还有平衡电桥，其中\(R_{1}\)为应变片电阻，\(R_{2}\)为可调电阻，调节\(R_{2}\)使得电桥平衡(检流计读数为 0)。这种方式由于需要人为将电桥调平衡，故只适用于静态测量

\[\frac{R_{1} + \Delta R_{1}}{R_{2} + \Delta R_{2}} = \frac{R_{3}}{R_{4}}\]

基于电桥的误差补偿

为了补偿温度带来的误差，需要设计补偿。一种是从结构上进行补偿，有单丝自补偿法和组合式自补偿法

单丝补偿法即通过调节参数匹配，使\(\alpha_\text{t} = -k(\beta_\text{g} - \beta_\text{s})\)。控制合金成分和退火温度可以控制\(\alpha_\text{t}\)，这种方法的温度适用范围有限，且材料通用性差。组合式自补偿法即串接不同金属丝，使得\(\Delta R_{1} = -\Delta R_{2}\)，只需\(\frac{\alpha_{1}}{\alpha_{2}} = -\frac{R_{2}}{R_{1}}\)即可。另一种从外部电路进行补偿，由于电阻变化值非常小，将应变片作为电阻接入电桥，将应变转化为电学量进行测量，下面详细介绍。

四个电桥电阻均会受到温度影响

\[\begin{aligned} U_\text{o}&=\frac{\frac{R_{2}}{R_{1}}}{(1 + \frac{R_{2}}{R_{1}})^2}\left(\frac{\Delta R_{1}}{R_{1}}-\frac{\Delta R_{2}}{R_{2}}+\frac{\Delta R_{4}}{R_{4}}-\frac{\Delta R_{3}}{R_{3}}\right)(1 - \eta)U\\ \eta&=\frac{1}{1+\frac{(1 + \frac{R_{2}}{R_{1}})}{\frac{\Delta R_{1}}{R_{1}}+\frac{\Delta R_{3}}{R_{3}}+\frac{R_{2}}{R_{1}}\left(\frac{\Delta R_{2}}{R_{2}}+\frac{\Delta R_{4}}{R_{4}}\right)}}U \\ &\frac{\Delta R_\text{i}}{R_\text{i}}\ll 1时，\eta = 0\\ U_\text{o}&=\frac{\frac{R_{2}}{R_{1}}}{(1 + \frac{R_{2}}{R_{1}})^2}\left(\frac{\Delta R_{1}}{R_{1}}-\frac{\Delta R_{2}}{R_{2}}+\frac{\Delta R_{4}}{R_{4}}-\frac{\Delta R_{3}}{R_{3}}\right)U\\ &=\frac{n}{(1 + n)^2}\left(\frac{\Delta R_{1}}{R_{1}}-\frac{\Delta R_{2}}{R_{2}}+\frac{\Delta R_{4}}{R_{4}}-\frac{\Delta R_{3}}{R_{3}}\right)U\\ 对于等臂电桥:U_\text{o} &=\frac{1}{4}\left(\frac{\Delta R_{1}}{R_{1}}-\frac{\Delta R_{2}}{R_{2}}+\frac{\Delta R_{4}}{R_{4}}-\frac{\Delta R_{3}}{R_{3}}\right)U \end{aligned}\]

从上式可得：输出电压正比于相对桥臂电阻变化率之和，相邻桥臂电阻变化率之差

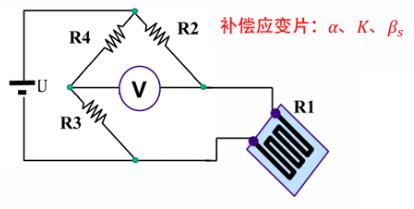
因此可以在相邻桥臂处粘贴补偿应变片但不施加应变，抵消掉工作应变片的温度误差

\[\begin{aligned} \frac{\Delta R_{1}}{R_{1}}&=\left(\frac{\Delta R_{1}}{R_{1}}\right)_{\varepsilon}+\left(\frac{\Delta R_{1}}{R_{1}}\right)_\text{t}\\ \frac{\Delta R_{2}}{R_{2}}&= 0+\left(\frac{\Delta R_{2}}{R_{2}}\right)_\text{t}\\ U_\text{o}&=\frac{1}{4}\left(\left(\frac{\Delta R_{1}}{R_{1}}\right)_{\varepsilon}+\left(\frac{\Delta R_{1}}{R_{1}}\right)_\text{t}-\left(\frac{\Delta R_{2}}{R_{2}}\right)_\text{t}+\frac{\Delta R_{4}}{R_{4}}-\frac{\Delta R_{3}}{R_{3}}\right)U\\ &=\frac{1}{4}k\varepsilon U_\text{i} \quad (只与应变有关，与温度无关) \end{aligned}\]

除了进行温度补偿，还可以采用双臂、四臂差动电桥提高测量灵敏度

\[\begin{aligned} \frac{\Delta R_{1}}{R_{1}}&=\left(\frac{\Delta R_{1}}{R_{1}}\right)_{\varepsilon}+\left(\frac{\Delta R_{1}}{R_{1}}\right)_\text{t}\\ \frac{\Delta R_{2}}{R_{2}}&=\left(\frac{\Delta R_{2}}{R_{2}}\right)_{-\varepsilon}+\left(\frac{\Delta R_{1}}{R_{1}}\right)_\text{t}\\ U_\text{o}&=\frac{1}{4}\left(\left(\frac{\Delta R_{1}}{R_{1}}\right)_{\varepsilon}-\left(\frac{\Delta R_{2}}{R_{2}}\right)_{-\varepsilon}+\frac{\Delta R_{4}}{R_{4}}-\frac{\Delta R_{3}}{R_{3}}\right)U\\ &=\frac{1}{4}(k\varepsilon - k(-\varepsilon))U=\frac{1}{2}k\varepsilon U_\text{i} \end{aligned}\]

有源单臂测量电桥

实质是一个比例求差电路

\[U_{0}=\frac{\frac{R_{3}}{R_{2}}}{\frac{R_{3}}{R_{2}}+1}(1 + \frac{R_{4}}{R_{1}})U_\text{i2}-\frac{R_{4}}{R_{1}}U_\text{i1}\]

假设，某一个\(R\)变为\(R + \Delta R\)

\[\begin{aligned} U_{0}&=(1 + \frac{R+\Delta R}{R})\frac{R}{R + R}U_\text{i}-\frac{R+\Delta R}{R}U_\text{i}\\ U_{0}&=-\frac{\Delta R}{2R}U_\text{i}=-\frac{1}{2}K\varepsilon U_\text{i} \end{aligned}\]

因此，相较于前面的普通直流电桥，有源单臂测量电桥是线性的、灵敏度是原来的两倍、输出电阻小负载能力强

特点

电阻应变片的使用：

1. 目测电阻应变片有无折痕.断丝等缺陷。
2. 用数字万用表测量应变片电阻值大小。同一电桥中各应变片之间阻值相差不得大于 0.5 欧姆
3. 试件表面处理：贴片处置用细纱纸打磨干净，用酒精棉球反复擦洗贴处，直到棉球无黑迹为止。
4. 应变片粘贴：在应变片基底上挤一小滴 502 胶水，轻轻涂抹均匀，立即放在应变贴片位置。
5. 焊线：用电烙铁将应变片的引线焊接到导引线上。
6. 用兆欧表检查应变片与试件之间的绝缘组织，应大于 500M 欧。
7. 保护：用 704 硅橡胶覆于应变片上，防止受潮。

电阻应变片的特点：

• 测量精度高，应变测量误差<1%
• 测量范围宽，几个\(\mu \varepsilon\)到上千\(\mu \varepsilon\)
• 分辨率高，一般\(1\mu \varepsilon\)
• 频率特性好，\(10^{-7}~10^{-10}s\)，(可测几百 kHz)
• 尺寸小，重量轻，对工件的应力分布基本无影响
• 环境适应性强
• 在大应变下，有较大非线性
• 输出信号微弱，抗干扰能力差
• 实际是敏感栅范围的平均应变
• 温度系数较大

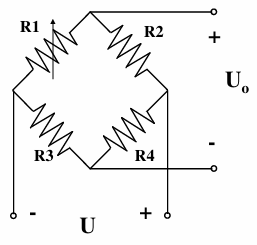
不同结构的弹性元件

柱形弹性元件：结构简单、紧凑、承受载荷大(最大\(10^7\text{N}\))

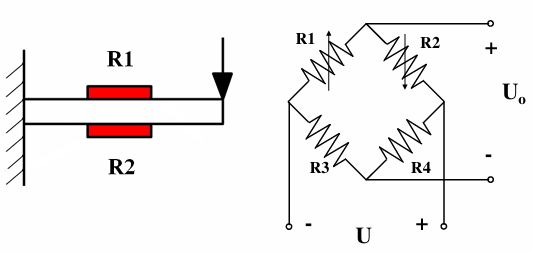
梁式弹性元件：结构简单、应变片易粘贴、灵敏度较高，适用于小载荷。有等截面型梁试件(应变片粘贴位置直接影响应变大小)和等强度梁(应变片粘贴位置不影响应变大小)

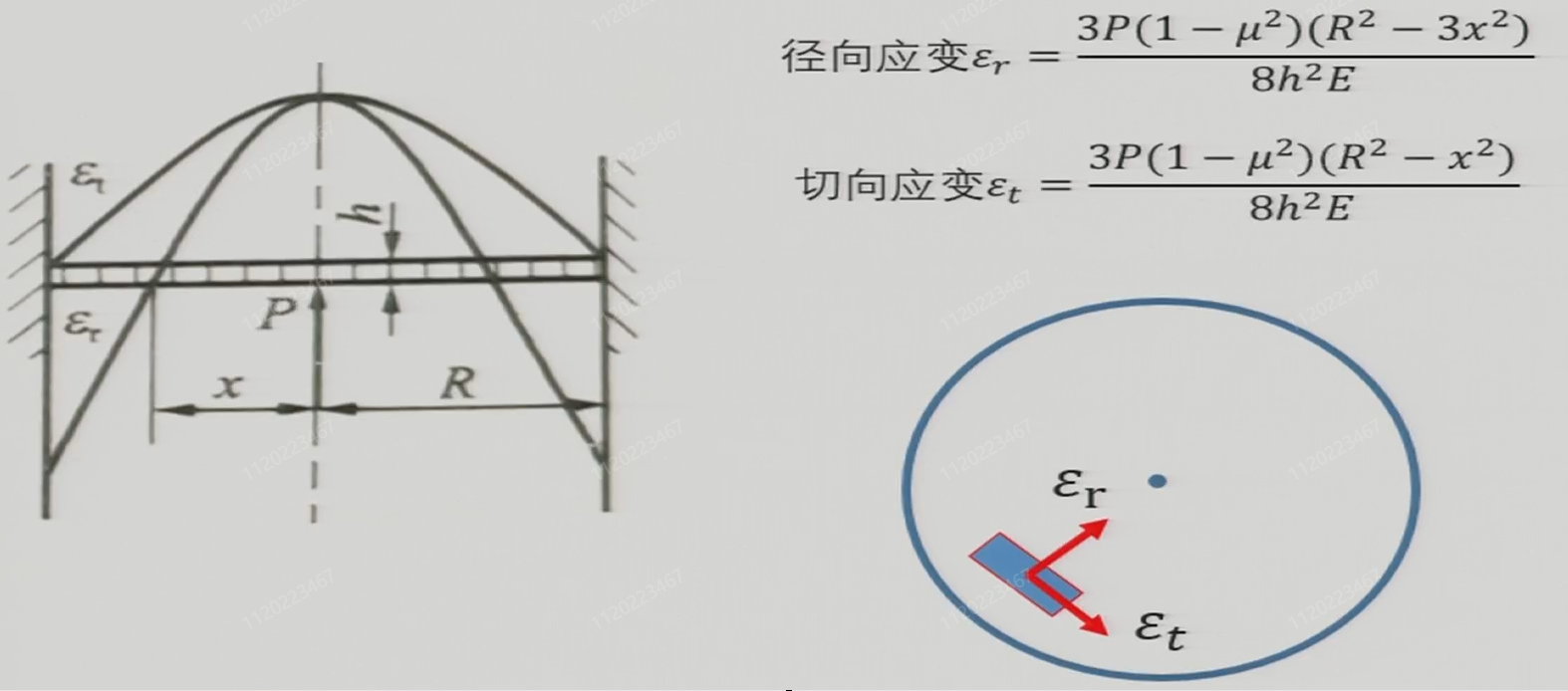
承弯膜片：

膜片式弹性元件：常用于测量内外压差，周边固定在壳体上

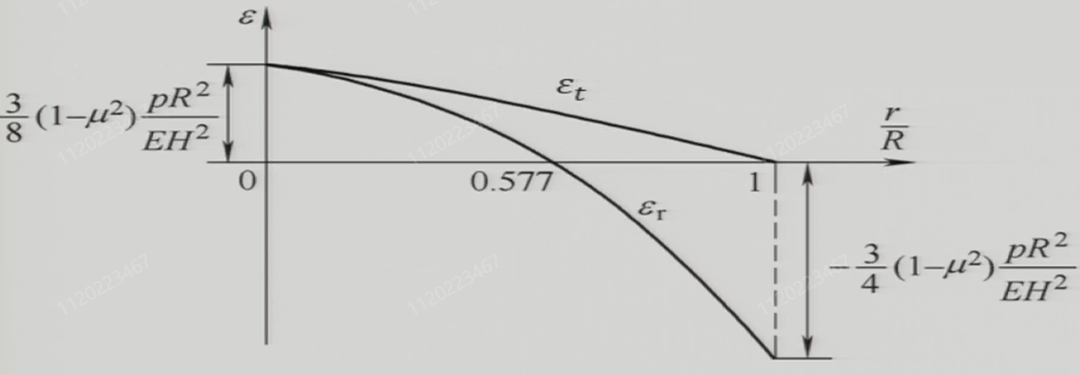
膜片应力分布特点：径向应变在膜片中心\(x=0\)处达到最大拉伸应变，随半径增大逐渐减小，至\(x=\frac{R}{\sqrt{3}}\)时为零，之后变为压缩应变，在边缘\(x=R\)处达到最大压缩应变。切向应变在中心处最大，始终为拉伸应变，随半径增加逐渐减小，至边缘\(x=R\)时降为零。整体表现为中心区域双向拉伸，外围径向应变转为压缩，切向应变始终为拉伸但逐渐减弱。如果使用两片应变片进行测量，应贴在应力变化较大且能反被测压力变化灵敏度最高的区域，两片应变片均沿径向方向粘贴，一片贴于中心\(x=0\)处，另一片贴于边缘\(x=R\)处，两应变片接入相邻桥臂(中心应变片阻值增大，边缘应变片阻值减小)。

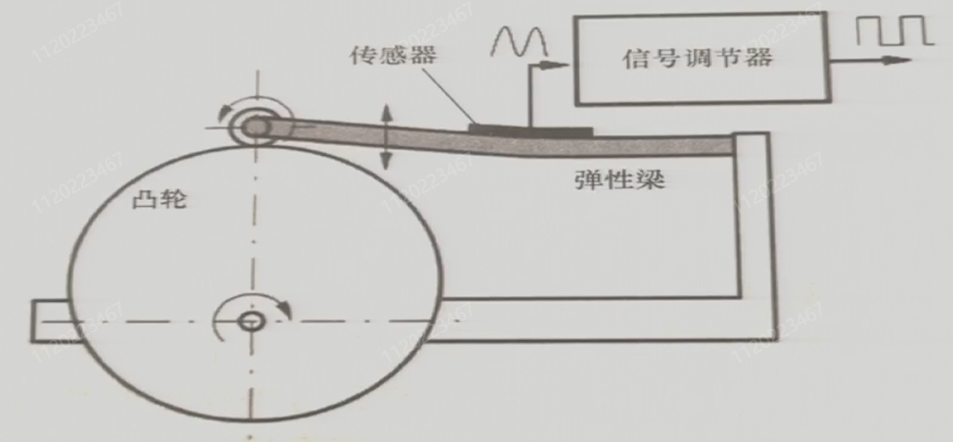
凸轮机构测量转速：(或使用连杆弹簧)

思路：

选则合适的弹性元件：柱状、梁式、膜片式

布置应变片位置：找到应力最大的方向，在此方向和垂直于此方向上粘贴应变片

连接电桥：承受相反应变的应变片放在相邻桥臂、承受相同应变的应变片放在相对桥臂

第三章 电感式传感器

以磁场作为媒介或利用铁磁体的某些现象，利用线圈自感或互感的变化来测量，核心部分是可变自感或可变互感，主要特征是具有线圈绕组。

3.1 自感式传感器

又称为变磁阻式传感器

工作原理

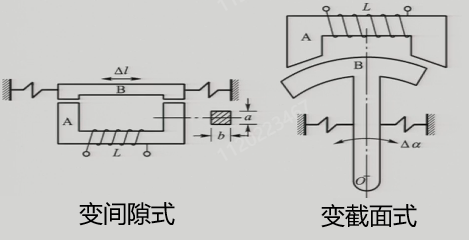
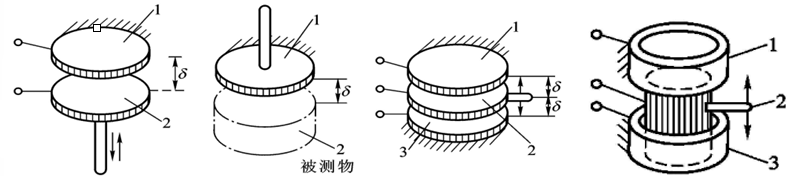
电感值与线圈匝数，线圈形状，导磁材料等都有关。基本原理为：衔铁摆动使得气隙磁阻变化，引起电感值的改变。以典型的单边自感式传感器为例，电感值与结构参数的关系如下，其中\(W\)为线圈匝数，\(\mu_{0} = 4\pi \times 10^{-7} \text{H/m}\)为真空导磁率，\(S_{0}\)为空气隙有效截面积，\(l_{0}\)为空气隙长度。

\[\begin{aligned} \Phi &= \frac{WI}{R_\text{m}} \quad (\frac{磁动势}{磁阻})\\ R_\text{m} &= \sum_\text{i=1}^n\frac{l_\text{i}}{\mu_\text{i} S_\text{i}} + 2\frac{l_\text{o}}{\mu_\text{o} S_\text{o}} \quad (\mu_\text{i} \gg \mu_\text{o})\\ L &= \frac{\Psi}{I} = \frac{W\Phi}{I} = \frac{W^2}{R_\text{m}} = \frac{W^{2}\mu_{0}S_{0}}{2l_{0}} \end{aligned}\]

这两种类型传感器的测量范围较小，测量范围较大的有螺线管自感式传感器。

差动自感式传感器：提高测量的线性度和灵敏度、对温度和电压波动进行补偿

性能指标

• 灵敏度：

  对于变间隙型，\(L\)反比于\(l\)，分析如下：

  \[\begin{aligned} L&=\frac{A}{l} \quad A = \frac{W^2 \mu_{0} S_{0}}{2}\\ \Delta L&=L - L_{0}=\frac{A}{l_{0}+\Delta l}-\frac{A}{l_{0}}\\ &=\frac{A}{l_{0}}\left(\frac{1}{1+\frac{\Delta l}{l_{0}}}-1\right)=L_{0}\left(\frac{1}{1+\frac{\Delta l}{l_{0}}}-1\right)\\ \Delta L&=-L_{0}\frac{\Delta l}{l_{0}}+L_{0}\left(\frac{\Delta l}{l_{0}}\right)^{2}\frac{1}{1+\frac{\Delta l}{l_{0}}} \approx -L_{0}\frac{\Delta l}{l_{0}}\\ 即&: 灵敏度K = -\frac{L_{0}}{l_{0}}\\ \end{aligned}\]

  因此，为了提高灵敏度和减小非线性误差，\(l_{0}\)和\(\Delta l\)都不能过大。同时，从式子可见，变间隙式传感器的灵敏度和线性度是矛盾的。

  对于差动式，分析如下：

  \[\begin{aligned} \Delta L_{1}&=-L_{0}\frac{\Delta l}{l_{0}}+L_{0}\left[\left(\frac{\Delta l}{l_{0}}\right)^2 - \left(\frac{\Delta l}{l_{0}}\right)^3 + \left(\frac{\Delta l}{l_{0}}\right)^4-\cdots\right]\\ \Delta L_{2}&=L_{0}\frac{\Delta l}{l_{0}}+L_{0}\left[\left(\frac{\Delta l}{l_{0}}\right)^2 + \left(\frac{\Delta l}{l_{0}}\right)^3 + \left(\frac{\Delta l}{l_{0}}\right)^4+\cdots\right]\\ \Delta L&=\Delta L_{1} - \Delta L_{2}=-2L_{0}\frac{\Delta l}{l_{0}}-2L_{0}\left(\frac{\Delta l}{l_{0}}\right)^3\left[1 + \left(\frac{\Delta l}{l_{0}}\right)^2 + \left(\frac{\Delta l}{l_{0}}\right)^4+\cdots\right]\\ \end{aligned}\]

  因此，灵敏度和线性度相较于单边型传感器均有所改善。另外差动式还可以实现温度补偿、电压波动补偿等；同时，传感器工作时对衔铁有一定吸引力，单边式传感器克服这种吸引力需要一定能量，双边式由于衔铁两侧受相反方向的吸引力，这种效应也会被抵消一些。

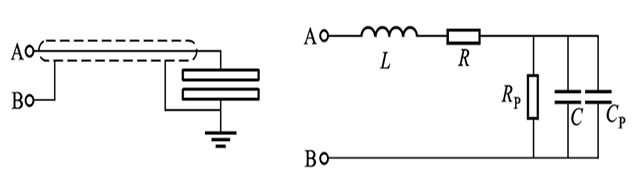
等效电路

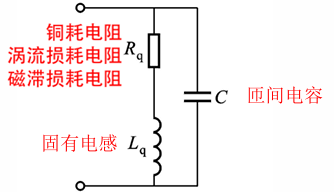
电感线圈等效电路如下：使用时根据工作频率考虑等效电路的影响

转换电路

转换电路将电感变化转化为电流电压的幅值、频率或相位变化，分别对应调幅、调频、调相电路

• 调幅电路：主要有电桥式和谐振式两种

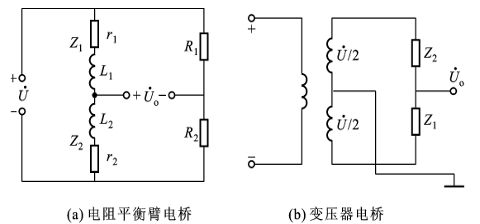
  (交流)电桥式转换电路的两种实用形式

  

  1. 电阻平衡臂电桥(\(Z_{1}\)为固定电感，\(Z_{2}\)变为\(Z_{2} + \Delta Z\)) \(\begin{aligned} Z&=r + \text{j}\omega L\\ |Z|&=\sqrt{r^2 + (\omega L)^2}\\ |\Delta Z|&=\frac{r\Delta r+\omega^2 L\Delta L}{\sqrt{r^2 + (\omega L)^2}}\quad (全微分，求偏导数得到)\\ \text{品质因数}Q &= \frac{\omega L}{r}\\ \dot{U}_\text{o}&=\left(\frac{Z_{2}}{Z_{1} + Z_{2}}-\frac{R}{R + R}\right)\dot{U}\\ &\approx\left(\frac{Z+\Delta Z}{2Z}-\frac{1}{2}\right)\dot{U}=\frac{\Delta Z}{2Z}\dot{U}\\ |U_\text{o}|&=\frac{|\Delta Z|}{|Z|}\cdot\frac{U}{2}\\ &=\left[\frac{r^2}{r^2 + (\omega L)^2}\frac{\Delta r}{r}+\frac{(\omega L)^2}{r^2 + (\omega L)^2}\frac{\Delta L}{L}\right]\cdot\frac{U}{2}\\ &=\frac{U}{2(1 + \frac{1}{Q^2})}\left(\frac{1}{Q^2}\frac{\Delta r}{r}+\frac{\Delta L}{L}\right)\quad \\ &\approx\frac{U}{2}\frac{\Delta L}{L}\quad(\text{当}Q\text{值很高时})\\ \end{aligned}\)
  2. 变压器电桥
  \[\begin{aligned} \dot{U}_\text{o}&=\frac{Z_{1}}{Z_{1} + Z_{2}}\dot{U}-\frac{1}{2}\dot{U}\\ \dot{U}_\text{o}&=\left(\frac{Z+\Delta Z}{2Z}-\frac{1}{2}\right)\dot{U}=\frac{\Delta Z}{2Z}\dot{U}\\ 其余&同上 \end{aligned}\]

  电桥式调幅电路，输出电压幅值表征位移大小，相位表征位移方向(注意不是输出极性相反)

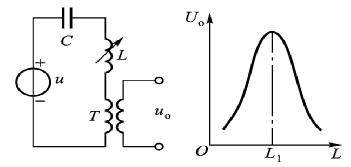
  谐振式调幅电路：串联谐振式调幅电路，令工作电源频率与电路谐振频率相等，此时阻抗最小，次级绕组输出最高的峰值电压。当 L 发生变化时，电路失谐，谐振峰左右移动，阻抗增加，输出电压幅值降低。特点是在小范围内具有高灵敏度

  \[f = \frac{1}{2\pi\sqrt{LC}}\]

  

• 调频电路

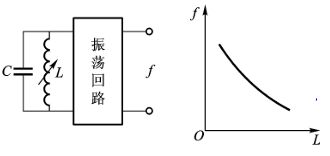
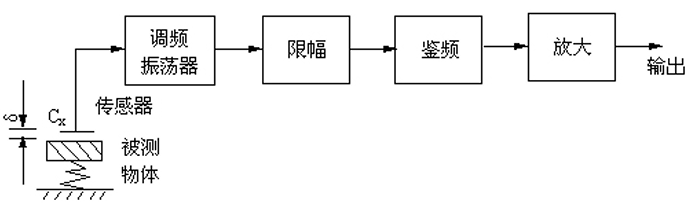
  传感器 L 和固定电容 C 接入一个振荡回路，L 变化时，根据 f 大小测出被测量值

\[\begin{aligned} f&=\frac{1}{2\pi\sqrt{LC}}\\ \Delta f&=-\frac{1}{4\pi}(LC)^{-\frac{3}{2}}C\cdot\Delta L=-\frac{f}{2}\cdot\frac{\Delta L}{L} \end{aligned}\]

• 调相电路

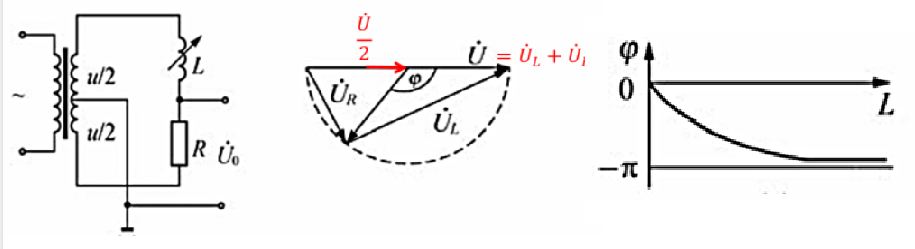
  原理是传感器电感 L 变化引起输出电压相位\(\varphi\)的变化

  

  \[\begin{aligned} \dot{U} &= \dot{U}_\text{L} + \dot{U}_\text{R}\\ \dot{U}_\text{o}&=\frac{R}{R + \text{j}\omega L}\dot{U}-\frac{1}{2}\dot{U}\\ &=\frac{R - \text{j}\omega L}{R + \text{j}\omega L}\cdot\frac{\dot{U}}{2}\\ \varphi &= \dot{U}_\text{o}\text{相角}-\dot{U}\text{相角}=-2\arctan\frac{\omega L}{R} \end{aligned}\]

  这种结构中，取导数可得\(\Delta L\)与\(\Delta \varphi\)的关系，而幅值不变

\[\Delta\varphi=\frac{2\left(\frac{\omega L}{R}\right)}{1 + \left(\frac{\omega L}{R}\right)^2}\cdot\frac{\Delta L}{L}\]

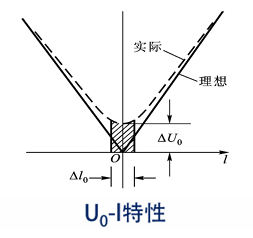
零点残余电压

差动式自感传感器衔铁在中间位置时，转换电路输出不为零，存在着某个输出值 △U0，整个成了非线性，且在零点附近存在一段死区，工作不灵敏，分辨率降低，这种现象称为零点残余电压。

产生原因：

• 两个传感器不对称(几何尺寸、电气参数、磁路参数)：提高加工精度
• 存在寄生参数：使用时进行屏蔽
• 电源存在高次谐波(因为是针对基波设计的电路)
• 磁路存在非线性：不要使激励电流过大，磁化曲线始终在线性区
• 工频干扰：抗干扰设计

磁化曲线非线性：激磁磁势超过了线性范围，产生的磁通被“削顶”，削顶波即由正弦基波和三次谐波组成

电位器调整零点残余电压(电气调零)，螺钉进行机械调零

特点

• 分辨率高，目前可测 0.1 从\(\mu m\)、0.1 角秒
• 测量范围比较小，适用于测量较小位移
• 存在非线性
• 消耗功率较大，尤其是单边式电感传感器
• 需要磁屏蔽：用磁性材料空腔包围自感式传感器，空腔内部不受外界磁场影响
• 限制在磁性材料的居里温度范围(居里点：磁性材料丧失磁性的温度)

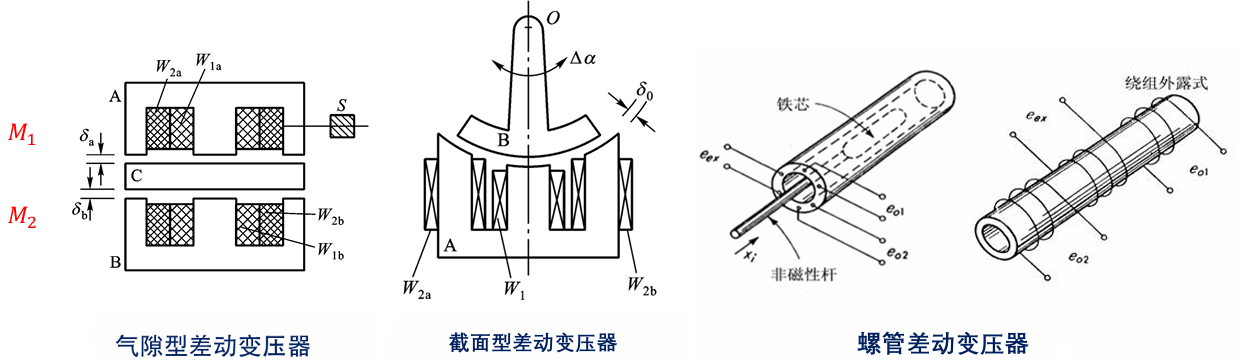
3.2 变压器式传感器

也称互感式传感器，通过检测互感系数的变化进行测量，简称 LVDT(linear variable differential transformer)

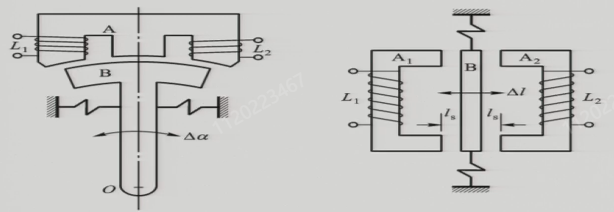
差动变压器结构与差动自感式变压器结构相似，但差动变压器铁芯上绕有疏密程度不同的线圈，上下各为一个变压器，共用中间衔铁形成磁路，衔铁移动引起上下变压器的互感系数发生改变。工业上应用较多的是螺管式差动变压器，螺线管由匝数不同的绕组构成。衔铁在螺线管中移动，使得绕组间的互感系数发生改变。

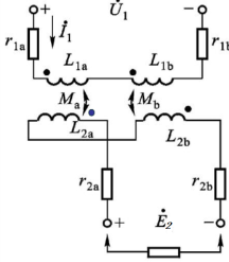
等效电路

将两个绕组的初级线圈串联(同名端不直接相连)，接入交流电源；而输出采用差动输出(同名端直接相连)。左侧为上面部分变压器，右侧为下面部分变压器。衔铁靠近哪一边，对应的互感系数便增大(铁芯有助于建立互感)，读取差动输出的电压便可得到位移的方向和大小。

\[\begin{aligned} \dot{E}_\text{2a}&=-\text{j}\omega M_\text{a} \dot{I}_{1}\quad\dot{E}_\text{2b}=-\text{j}\omega M_\text{b} \dot{I}_{1}\\ M_\text{a}&=\frac{W_\text{1a}W_\text{2a}}{R_\text{ma}}\quad M_\text{b}=\frac{W_\text{1b}W_\text{2b}}{R_\text{mb}}\\ Q&=\frac{\omega L}{r}\\ \text{假设：}W_\text{1a}&=W_\text{2a}=W_{1},\ r_\text{1a}=r_\text{1b}=r_{1}\\ W_\text{1b}&=W_\text{2b}=W_{2},\ L_\text{1a0}=L_\text{1b0}=L_{10}\\ \dot{E}_{2}&=\dot{E}_\text{2a}-\dot{E}_\text{2b}=-\text{j}\omega\dot{I}_{1}(M_\text{a} - M_\text{b})\\ &=\dot{U}_{1}\cdot\frac{W_{2}}{W_{1}}\cdot\frac{\Delta l}{l_{0}}\cdot\frac{1 + j\frac{1}{Q}}{1+\frac{1}{Q^{2}}}\\ \vert \dot{E_{2}} \vert &=U_{1}\frac{W_{2}}{W_{1}}\frac{\Delta l}{l_{0}}\frac{1}{\sqrt{1+\frac{1}{Q^{2}}}} \end{aligned}\] \[\begin{cases} \text{当}\omega L_{10}\ll r_{1}\text{时，}Q\ll1,\text{灵敏度}K = U_{1}\frac{W_{2}}{W_{1}}\frac{1}{l_{0}}\frac{\omega L_{10}}{r_{1}}\\ \text{当}\omega L_{10}\gg r_{1}\text{时，}Q\gg1,\text{灵敏度}K = U_{1}\frac{W_{2}}{W_{1}}\frac{1}{l_{0}}\\ \end{cases}\]

由式可见：

• 供电电源要稳定；电源幅值适当提高可提高灵敏度，但要以铁芯不饱和允许温升为条件。
• 增加\(\frac{W2}{W1}\) 和减小\(l_{0}\)都能使灵敏度 K 值提高。(\(\frac{W2}{W1}\)影响体积及零点残余电压，一般\(l_{0}\)为 0.5mm)

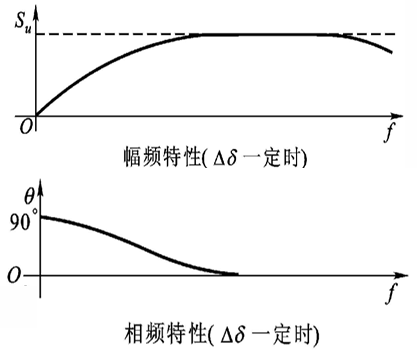
另外，随着频率升高，铁磁材料的铁损增大，K、Q 下降。因此需要找到一个合适的工作频率，一般来说，对于差动变压器式传感器，上下限截止频率限制的范围在 400Hz-10kHz 之间。

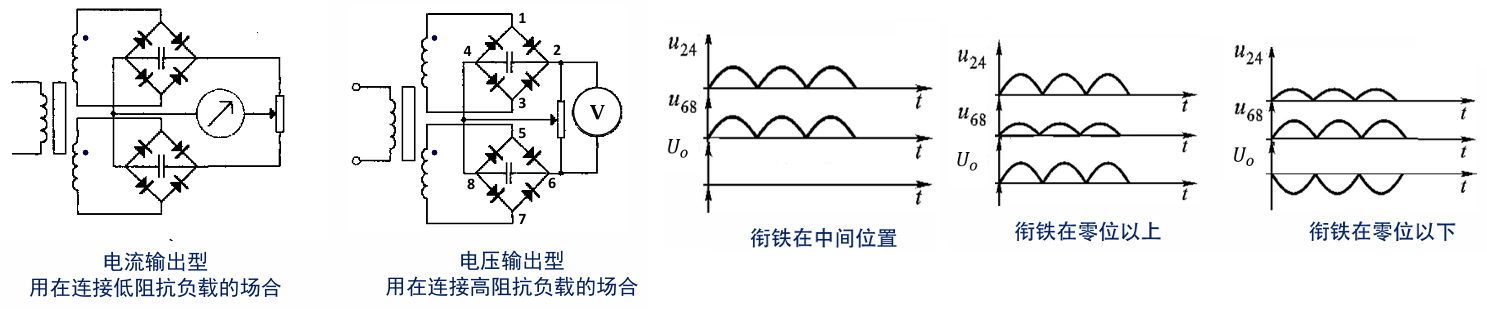
测量电路

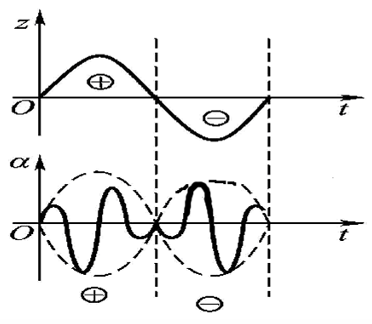
分析：当输入为正弦波时，输出为以被测量为包络线的调幅波，注意输入反向时，输出相位变化\(180°\)

测量电路需要解决的，就是位移方向和大小的测量，因此需要鉴别相位，同时需要消除零点残余电压，一般采用差动整流电路：\(\dot{U}_{0}=\dot{U}_{24}-\dot{U}_{68}\)，输出的\(U\_\text{o}\)为双极性电压，通过极性就可以判断位移方向。

零点残余电压的消除，一方面需要尽量使传感器本身的尺寸和电气参数、磁路参数等很好地对称；另一方面可以通过补偿电路尽可能抵消其影响。

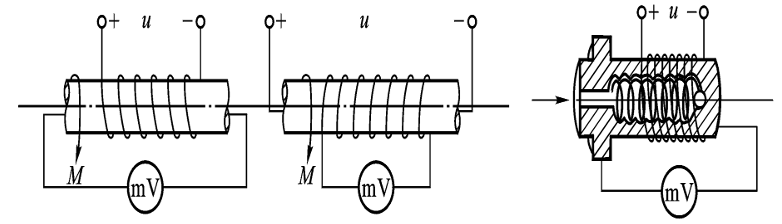
3.3 涡流式传感器

左侧为高频反射式传感器，右侧为低频透射式传感器

高频反射式涡流传感器

线圈的交变电流产生磁场\(\Phi_{1}\)，磁场\(\Phi_{1}\)在金属体内产生感生电流/涡流以阻碍\(\Phi_{1}\)的变化(交流电线圈和金属体之间的互感效应)，使得金属体的阻抗发生改变。金属导体作为被测对象，可以利用该性质进行测量。

涡流的大小与线圈尺寸、激励电流大小和频率有关，也与金属电阻率、磁导率、金属与线圈之间的距离等有关

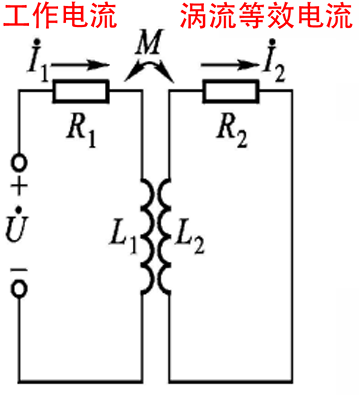
涡流通过反射阻抗作用改变阻抗，将金属体看作一匝闭合短路的线圈

\[\begin{aligned} &R_{1}\dot{I}_{1} + \text{j}\omega L_{1}\dot{I}_{1} - \text{j}\omega M\dot{I}_{2} = \dot{U} \\ &R_{2}\dot{I}_{2} + \text{j}\omega L_{2}\dot{I}_{2} - \text{j}\omega M\dot{I}_{1} = 0 \\ &Z = R_{1} + R_{2}\frac{\omega^2 M^2}{R_{2}^2 + \omega^2 L_{2}^2}+\text{j}\omega\left(L_{1} - L_{2}\frac{\omega^2 M^2}{R_{2}^2 + \omega^2 L_{2}^2}\right) \end{aligned}\]

其中，\(R_{1} + R_{2}\frac{\omega^2 M^2}{R_{2}^2 + \omega^2 L_{2}^2}\)称为等效电阻，\(R_{2}\frac{\omega^2 M^2}{R_{2}^2 + \omega^2 L_{2}^2}\)称为反射电阻；\(L_{1} - L_{2}\frac{\omega^2 M^2}{R_{2}^2 + \omega^2 L_{2}^2}\)称为等效电感，\(L_{2}\frac{\omega^2 M^2}{R_{2}^2 + \omega^2 L_{2}^2}\)称为反射电感。对于非磁性材料而言，当金属导体和线圈靠近时，涡流效应使得等效电阻增加，有功损耗增大，同时等效电感减小，无功损耗减小，表现为去磁作用；对于磁性材料而言，靠近过程中自感系数\(L_{1}\)会显著增大，表现为增磁作用。

显然，两个反射量都是互感系数\(M\)的函数，而\(M\)与线圈和金属导体之间的距离、金属本身的电阻率\(\rho\)以及磁导率\(\mu\)有关，因此，改变间距可测量位移、厚度；改变电阻率可测量温度；改变磁导率可测量硬度。(硬度高，内部应力大，位错密度高，阻碍磁畴运动，使得磁导率下降)

转换电路

• 调幅电路：同前面的电桥和谐振调幅电路

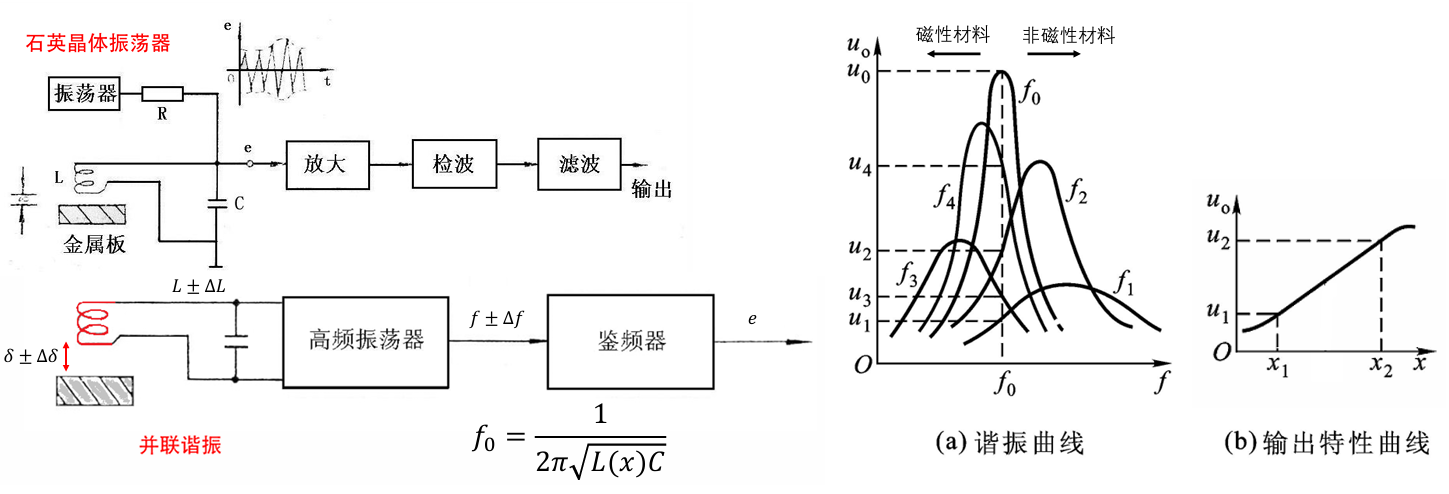
• 调频电路：谐振调幅电路，阻抗变化使得线圈阻值变化，并通过谐振频率的偏移反应在输出信号的幅值上。采用并联谐振的方式，谐振时阻抗最高，对应输出电压最高。当电路谐振频率不等于石英晶振振荡源提供的频率\(f_{0}\)(也称初始谐振频率)时，称为失谐。

  

  对于磁性材料，随着线圈与金属体的靠近，自感系数升高，谐振频率降低，阻抗降低，输出幅值下降；对于非磁性材料，随着线圈与金属体的靠近，自感系数降低，谐振频率增加，阻抗降低，输出幅值下降。(在\(f = f_{0}\)处读取输出信号幅值)

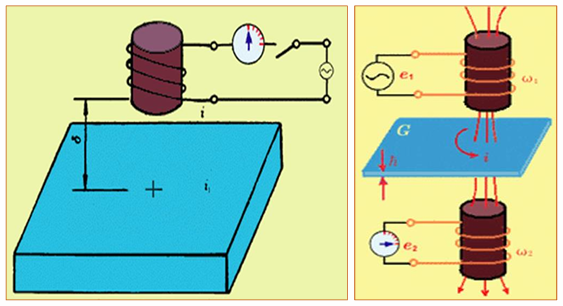
低频透射式涡流传感器

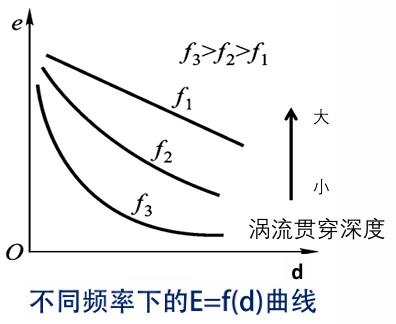
一组为工作线圈，另一组为测量线圈，用于测量工作线圈产生的交变感应电动势。在两组线圈之间介入金属导体，金属导体的厚度变化时，导体所受的磁通变化，引起输出的感应电动势相应改变。涡流的贯穿深度随涡流频率变化的关系如下，其中\(\rho\)为导体电阻率，\(\mu_\text{r}\)为导体相对磁导率，\(f\)为交变磁场频率

\[\begin{aligned} h &= 5030\sqrt{\frac{\rho}{\mu_\text{r} f}}\\ E &= kU_\text{i} \text{e}^{-\frac{d}{h}}\\ \end{aligned}\]

可见，交变磁场频率越低，测量范围越宽；为了测量厚度变化，需要使用低频电源；而测量表面缺陷或是很薄材料的厚度时，使用高频电源。低频的优点在于测量范围宽，高频的优点在于测量灵敏度高。另外，由于温度对电阻率有影响，因此也需要考虑如何进行温度补偿，或设计恒温的工作状态。

涡流传感器的特点

1. 探头无磁性材料，可以高温工作
2. 不受非导磁材料影响(油、灰尘、水)
3. 非接触测量，无磨损
4. 结构简单，安装方便

典型测量范围为 0.5mm-60mm，分辨率为 0.1um

3.4 压磁式传感器

工作原理

压磁式传感器的工作原理基于压磁效应和磁致伸缩效应：

• 压磁效应：某些铁磁物质在外界机械力的作用下，其内部产生机械应力，从而引起磁导率的改变。材料受到压力时，在作用力方向磁导率减少；在与作用力垂直方向磁导率略有增加；材料受到拉力时，效果相反，这称为压磁效应的各向异性。外界作用力取消后磁导率复原。且实验表明，压磁效应还与外磁场有关，为保证磁导率与应力的单值关系，必须使外磁场强度恒定。
• 磁致伸缩效应：某些铁磁物质在外界磁场的作用下会产生拉伸或压缩的形变

灵敏度表示方法

对于压磁式传感器，灵敏度即为单位应变对应的磁导率的相对变化

• 压磁应变灵敏度：\(S = \frac{\varepsilon_{\mu}}{\varepsilon_\text{l}}=\frac{\Delta \mu / \mu}{\Delta l / l}\)
• 压磁应力灵敏度：\(S_{\sigma}=\frac{\Delta\mu/\mu}{\sigma}\)

其中，\(\frac{\Delta\mu}{\mu}=\frac{2\varepsilon_\text{s}}{B_\text{S}^2}\sigma\mu\)，\(\varepsilon_\text{s}\)为材料的饱和应变，\(B_\text{s}\)为材料的饱和磁感应强度。当外界施加机械力时，会引起材料磁导率的变化，引起磁路磁阻的变化，从而影响磁路中线圈阻抗的变化或输出电势的变化

结构形式

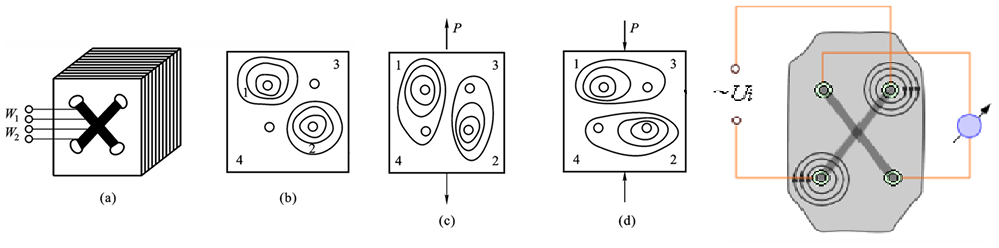
• 利用一个方向磁导率的改变：受力使得磁导率改变，引起互感变化，阻抗变化，使得输出电压发生变化

  \[\begin{aligned} L &= K_{1}u = K_{2}P\\ E_{2} &= \frac{W_{1}}{W_{2}}K(P)U_{1}P\\ \end{aligned}\]

• 利用两个方向磁导率的改变：利用各向异性来设计，一个对角线工作电流，另一个对角线测量电流，两线圈相互垂直。不受外力时，激励线圈建立的磁通不与测量线圈铰链。受压力作用后，磁导率的分布产生各向异性，椭圆的磁力线会穿过线圈，测量线圈中产生感应电动势即可获得材料所受的压力。受力越大，铰链的磁链越大。作用力方向的电压减小，垂直方向的电压略增加，部分磁力线与测量线圈铰链而产生感应电动势

  

• 利用维捷曼效应测量扭矩：棒状铁磁性物质被扭转时，棒中出现按螺旋分布的区域，电压沿螺旋方向增加，将铁磁棒其置于磁场中，磁畴就随着扭矩造成的螺旋区域排列，棒中即产生螺旋分布的磁通(可视为轴向磁通与旋转磁通的合成)

  

  以第一个图为例，未受力时磁通仅有轴向分量，受力后磁通产生旋转分量，会反映在穿过线圈的电动势输出上。冲片结构的形式有多种，目的包括提高灵敏度、提高测量范围、改善线性特性

特点和应用

压磁传感器的特点：

• 输出功率大，信号强
• 结构简单，牢固可靠
• 制作工艺简单，成本低
• 过载能力强
• 测量准确度不高，反应速度较低

技术和理论的不成熟点在于磁性材料的选择、磁性材料的热处理、励磁方式的选择以及输出特性的分析。压磁传感器常用于矿山、冶金、运输等工业部门作为测力和称重仪器，耐过载能力强，一般是对大量程的力进行测量，如起重运输的过载保护系统、轧钢压力及钢板厚度的控制系统、铁路车辆载货重量的称重系统等。缺点是测量准确度不高，反应速度较低，不适合于快速变化力的测量。

第四章 电容式传感器

电容式传感器结构简单，且不容易受外界温湿度的影响，但由于传感器本身的电容很小而环境中的分布电容和寄生电容较大，对传感器会产生严重的测量噪声干扰，直到后来解决了分布电容和寄生电容对传感器测量噪声的影响，电容式传感器才得到广泛应用。

4.1 工作原理及类型

电容的计算式为\(C = \frac{\varepsilon S}{d}\)，改变三个参数都可以改变电容容值

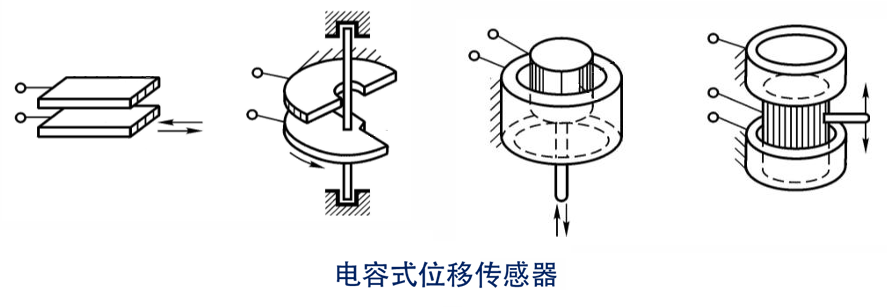
电容式传感器的类型：

• 基本类型：变极距型、变面积型、变介电常数型

• 电极形状：平板形、圆筒形、球面形等

• 单边结构、差动结构

以测位移的传感器为例，\(\Delta x \to \Delta d \to \Delta C\)

4.2 灵敏度及非线性

变极距型平板电容传感器的灵敏度

\[\begin{aligned} C_{0}&=\frac{\varepsilon S}{d_{0}}\\ C&=\frac{\varepsilon S}{d}\\ C&=\frac{\varepsilon S}{d_{0}+\Delta d}=C_{0}+\Delta C\\ \Delta C&=-\frac{C_{0}}{d_{0}}\Delta d + C_{0}\left(\frac{\Delta d}{d_{0}}\right)^2\left[1 - \left(\frac{\Delta d}{d_{0}}\right) + \left(\frac{\Delta d}{d_{0}}\right)^2\cdots\right]\\ k&=\frac{\Delta C}{\Delta d}=-\frac{C_{0}}{d_{0}}\left[1 - \left(\frac{\Delta d}{d_{0}}\right) + \left(\frac{\Delta d}{d_{0}}\right)^2\cdots\right] \end{aligned}\]

可见，灵敏度规律与自感式传感器类似，线性度和灵敏度对传感器的结构要求是矛盾的：只有比值\(\frac{\Delta d}{d_{0}}\)很小时才可认为是接近线性关系。可适当增大初始距离\(d_{0}\)，以保证比值\(\frac{\Delta d}{d_{0}}\)不致过大；但灵敏度下降，电容传感器初值减小。常采用差动式电容传感器。

差动式电容传感器

\[\begin{aligned} C_{1}&=C_{0}\frac{1}{1 - \frac{\Delta d}{d_{0}}} \quad C_{2} = C_{0}\frac{1}{1 + \frac{\Delta d}{d_{0}}}\\ C_{1}&=C_{0}\left[1 + \left(\frac{\Delta d}{d_{0}}\right) + \left(\frac{\Delta d}{d_{0}}\right)^2 + \left(\frac{\Delta d}{d_{0}}\right)^3 + \cdots\right]\\ C_{2}&=C_{0}\left[1 - \left(\frac{\Delta d}{d_{0}}\right) + \left(\frac{\Delta d}{d_{0}}\right)^2 - \left(\frac{\Delta d}{d_{0}}\right)^3 + \cdots\right]\\ \Delta C&=C_{1} - C_{2} = C_{0}\left[2\left(\frac{\Delta d}{d_{0}}\right) + 2\left(\frac{\Delta d}{d_{0}}\right)^3 + 2\left(\frac{\Delta d}{d_{0}}\right)^5 + \cdots\right]\\ \frac{\Delta C}{C_{0}}&=2\frac{\Delta d}{d_{0}}\left[1 + \left(\frac{\Delta d}{d_{0}}\right)^2 + \left(\frac{\Delta d}{d_{0}}\right)^4 + \left(\frac{\Delta d}{d_{0}}\right)^6 + \cdots\right] \end{aligned}\]

与自感式传感器类似，差动式结构可以同时改善灵敏度和线性度

变面积型电容器

平板型电容器：\(C=\frac{\varepsilon_{0}\varepsilon_\text{r} (a - \Delta x)b}{d}\)，\(\frac{\Delta C}{C_{0}}=\frac{\Delta x}{a}\)

圆柱形电容器：\(C = \frac{2\pi\varepsilon_{0}\varepsilon_\text{r} l}{\ln\frac{R}{r}}\)

变介电常数型电容器

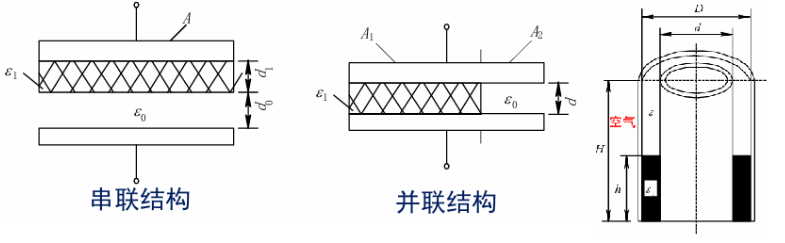
串联结构：

\[\begin{aligned} C&=\frac{C_{1}\cdot C_{2}}{C_{1} + C_{2}}=\frac{\varepsilon_{0}\varepsilon_{1} A}{\varepsilon_{1} d_{0} + d_{1}}\\ C_{0}&=\frac{\varepsilon_{0} A}{d_{0} + d_{1}}\\ \Delta C&=C - C_{0} = C_{0}\cdot\frac{\varepsilon_{1} - 1}{\varepsilon_{1}\frac{d_{0}}{d_{1}}+1} \end{aligned}\]

并联结构：

\[\begin{aligned} C&=C_{1} + C_{2}=\frac{\varepsilon_{0}\varepsilon_{1} A_{1} + \varepsilon_{0} A_{2}}{d}\\ C_{0}&=\frac{\varepsilon_{0}(A_{1} + A_{2})}{d}\\ \Delta C&=C - C_{0}=\frac{\varepsilon_{0} A_{1}(\varepsilon_{1} - 1)}{d} \end{aligned}\]

圆柱形结构

\[\begin{aligned} C_{0}&=\frac{2\pi\varepsilon_{0} H}{\ln\frac{D}{d}}\\ C&=C_{1} + C_{2}\\ &=\frac{2\pi\varepsilon_{0} (H - h)}{\ln\frac{D}{d}}+\frac{2\pi\varepsilon_{0}\varepsilon_{1} h}{\ln\frac{D}{d}}\\ &=\frac{2\pi\varepsilon_{0} H}{\ln\frac{D}{d}}+\frac{2\pi\varepsilon_{0} h(\varepsilon_{1} - 1)}{\ln\frac{D}{d}}\\ \Delta C&=C - C_{0}=\frac{2\pi\varepsilon_{0} h(\varepsilon_{1} - 1)}{\ln\frac{D}{d}} \end{aligned}\]

变极距电容传感器具有非线性特性，变面积型和变介电常数型(测厚除外)电容传感器具有很好的线性(忽略边缘效应)。实际上由于边缘效应仍存在非线性问题，且灵敏度下降。

4.3 特性与等效电路

特点

优点

1. 温度稳定性好

2. 结构简单、适应性强

   • 金属电极、无机材料(玻璃、石英、陶瓷等)绝缘支承

   • 可在高低温、强辐射、强磁场等恶劣环境下工作
   • 承受很大的温度变化、高压力、高冲击

3. 动态响应好

   • 可动部分质量很轻，极板间静电引力很小，需要作用的能量极小(可测量极小的压力、力、加速度、位移)，灵敏、分辨力高
   • 固有频率高，能在几 MHz 频率下工作，适于动态测量(振动、瞬间压力)

4. 可以实现非接触测量

   • 回转轴的振动或偏心
   • 小型滚珠轴承的径向间隙测量具有平均效应，减小工件表面粗糙度的影响

5. 高分辨率：在位移测量时已经达到 10pm 的分辨率，可以进行应变的测量

6. 本身不产生强磁场或强电场。而电感传感器可能产生强杂散磁场。

缺点：

1. 输出阻抗高(电容越小，容抗越大) ，负载能力差；易被干扰；对绝缘电阻要求高
2. 寄生电容影响大
   • 极板与周围导体的耦合电容
   • 测量电路的杂散电容
   • 引线电缆电容
   • 降低灵敏度；随机变化，使传感器工作不稳定
3. 输出特性非线性

等效电路

灵敏度与工作频率和引线电感有关，改变任意一个都需要对传感器的灵敏度重新标定

\[\begin{aligned} \frac{1}{\text{j}\omega C_\text{e}}&=\text{j}\omega L+\frac{1}{\text{j}\omega C}\\ C_\text{e}&=\frac{C}{1 - \omega^{2}LC}\\ K_\text{e}&=\frac{\Delta C_\text{e}}{\Delta d}=\left(\frac{1}{\frac{1}{C}-\omega^{2}L}\right)'K = \frac{K}{(1 - \omega^{2}LC)^{2}} \end{aligned}\]

4.4 设计要点

1. 提高传感器的电容值：降低输出阻抗；减轻对绝缘的要求；提高灵敏度

2. 减小温度、湿度对测量的影响

   

3. 消除和减小边缘效应：边缘效应使灵敏度降低，产生非线性。

   • 增大极板直径/边长间距比
   • 减小极板厚度间距比
   • 设计等位环结构

4. 消除和减小寄生电容的影响：寄生电容与传感器电容相并联，影响传感器的灵敏度，其变化则为虚假信号影响仪器的精度。

   • 增加原始电容值
   • 将传感器接地和屏蔽
   • 将传感器与测量线路前置级集成安装，省去传感器至前置级的电缆
   • 采用双层屏蔽等电位传输的驱动电缆

5. 防止和较小外界干扰：

   • 屏蔽和接地
   • 增加原始电容值以降低容抗
   • 导线和导线要离得远，以减小导线间分布电容的静电感应。导线要尽可能短，最好成直角排列，必须平行排列时可采用同轴屏蔽线
   • 尽可能一点接地，避免多点接地。地线要用粗的良导体或宽印刷线
   • 尽量采用差动式电容传感电路，可减小非线性误差，提高传感器灵敏度，减小寄生电容的影响和干扰。

4.5 转换电路

调制型电路

调制型电路有调幅电路和调频电路

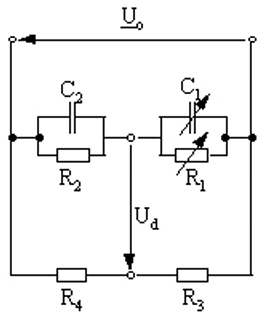
• 电桥测量电路

  

  \[\begin{aligned} \frac{\frac{R_{2}}{\text{j}\omega C_{2}}}{R_{2}+\frac{1}{\text{j}\omega C_{2}}}R_{3}&=\frac{\frac{R_{1}}{\text{j}\omega C_{1}}}{R_{1}+\frac{1}{\text{j}\omega C_{1}}}R_{4}\\ R_{2}R_{3}+\text{j}\omega R_{1}R_{2}R_{3}C_{1}&=R_{1}R_{4}+\text{j}\omega R_{1}R_{2}R_{4}C_{2}\\ 实部: R_{2}&=\frac{R_{4}}{R_{3}}R_{1}\\ 虚部: C_{2}&=\frac{R_{4}}{R_{3}}C_{1} \end{aligned}\]

• 调频电路

  

脉冲型电路

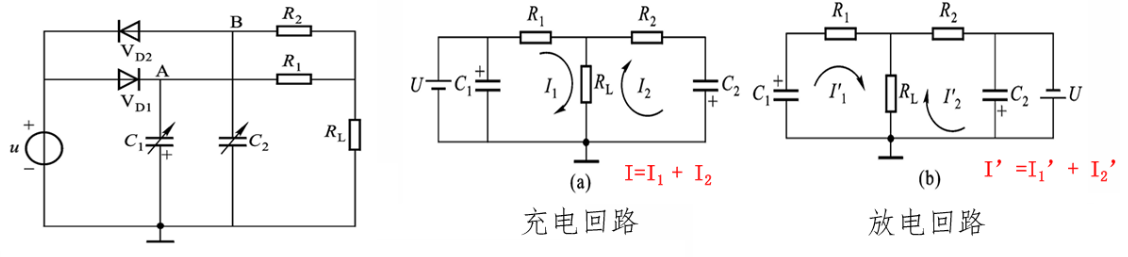
利用电容的充放电，有双 T 型充放电网络和脉冲调宽型电路

• 双 T 型充放电网络

  

  \[\begin{aligned} \text{时间常数}\tau&=(R+\frac{R_\text{L}R}{R_\text{L}+R})C_{2}\\ i_\text{C2}&=\left(\frac{U+\frac{R_\text{L}}{R_\text{L}+R}U}{R+\frac{RR_\text{L}}{R_\text{L}+R}}\right)\text{e}^{\frac{-t}{(R+\frac{R_\text{L}R}{R_\text{L}+R})C_{2}}}\\ I_\text{C2}&=\frac{1}{T}\int_{0}^{\frac{T}{2}}i_\text{C2}\text{d}t\approx\frac{1}{T}\int_{0}^{\infty}i_\text{C2}\text{d}t=\frac{1}{T}\frac{R + 2R_\text{L}}{R+R_\text{L}}UC_{2}\\ I_\text{C1}&=\frac{1}{T}\frac{R + 2R_\text{L}}{R+R_\text{L}}UC_{1}\\ U_{0}&=\frac{RR_\text{L}}{R + R_\text{L}}(I_\text{C1}-I_\text{C2})=\frac{RR_\text{L}(R + 2R_\text{L})}{(R+R_\text{L})^{2}}\frac{U}{T}(C_{1}-C_{2})\\ &=K\cdot U\cdot f\cdot(C_{1}-C_{2}) \end{aligned}\]

  特点：

  • 电路简单，易于集成
  • 灵敏度正比于电源幅值、频率，需要稳幅、稳频
  • 输出电压较高
  • 输出阻抗与 R1 或 R2 同数量级，与电容 C1 和 C2 无关
  • 适用于线性特性的电容传感器或差动式电容传感器。

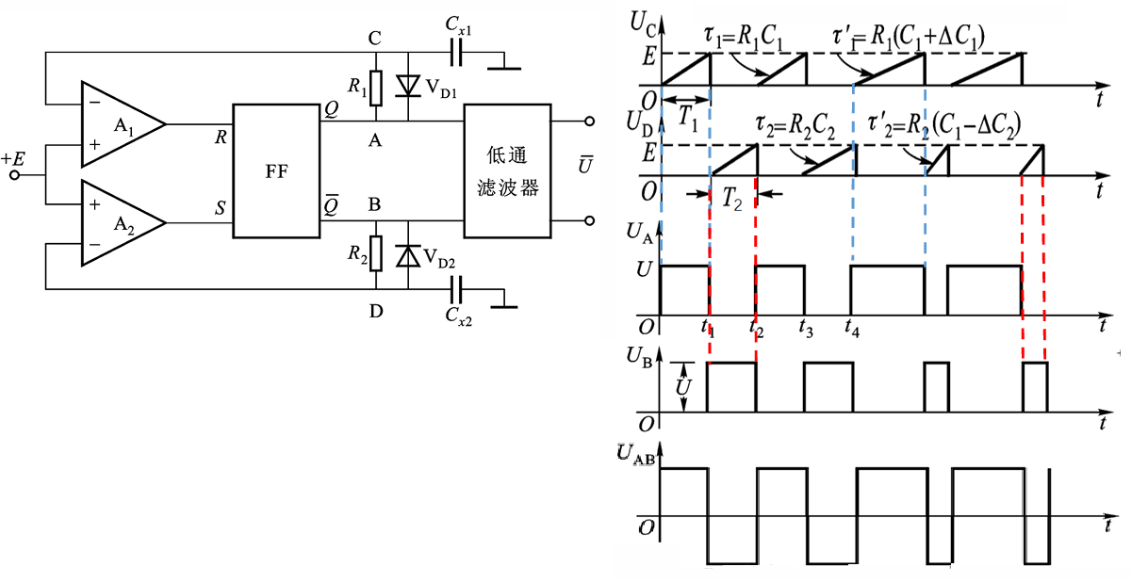
• 差动脉冲调宽型电路

  

  \[\begin{aligned} \frac{U_\text{c}}{U_\text{d}}&=U(1 - \text{e}^{-\frac{t}{\tau_{1}}})\\ T_{1}&=R_{1}C_{1}\ln\frac{U}{U - E}\\ T_{2}&=R_{2}C_{2}\ln\frac{U}{U - E}\\ u_{0}&=(u_\text{AB})_{\text{DC}} = u_\text{A}-u_\text{B}\\ &=\frac{T_{1}}{T_{1}+T_{2}}u_{\text{Am}}-\frac{T_{2}}{T_{1}+T_{2}}u_{\text{Bm}}\\ &=\frac{C_{1}-C_{2}}{C_{1}+C_{2}}u_\text{m}\\ \text{变极距型: }U_{0}&=\frac{d_{2}-d_{1}}{d_{2}+d_{1}}U \to u_{0}=\pm\frac{\Delta d}{d_{0}}u_\text{m}\\ \text{变面积型: }u_{0}&=\pm\frac{\Delta A}{A_{0}}u_\text{m} \end{aligned}\]

  特点：

  • 适用于差动式电容传感器，具有线性特性
  • 采用直流电源，电压稳定度高，不需要稳频
  • 经低通滤波器可输出较大的直流电压，对输出矩形波纯度要求不高