基于系统辨识的自动参数整定

为了节约电控用于整定 PID 参数的时间，以及方便以后使用依赖于模型的控制器，需要对机器人进行建模。本文以步兵 yaw 轴云台为例给出一个 demo，分步骤讲解如何在机器人上使用系统辨识以及自动参数整定

本系统辨识方案受官方系统辨识教程启发：官方开源教程-系统辨识基础教程

方案简述

希望辨识出以电机电流为输出，电机角速度为输出的开环传递函数模型，以便在 simulink 中使用。需要采集电机带负载在正常工况下的频率响应和阶跃响应，且为了消除随机误差，建议在不同时间，将机器人以不同方位放置在车架上进行测试。

经过尝试，如果辨识角度的传递函数，电机由于惯性，在不施加任何控制算法时，难以保证电机同一零点附近摆动，采集数据后需要进行复杂的数据处理工作，且效果不佳；故测试以角速度为输出的传递函数，由于仿真环境中是理想模型，对其积分即可得到角度。

数据采集

把车放在架子上，架子用桌子夹住，测试时按住底盘，尽量减小底盘的晃动，分别采集频率响应和阶跃响应数据

考虑到云台的转动惯量和实际工况，频率响应采集的频率范围为 1~10Hz，中间每 0.5Hz 一档，电流幅值为 6000

阶跃响应的电流范围为 0~15000(正负交替)

系统辨识所涉及的代码如下

#define RESPONSE_MODE FREQ_RESPONSE

float openloop_spd_ref = 0.0f;
float openloop_spd_fdb = 0.0f;
int openloop_spd_amplitude = 6000.0f;

// 阶跃信号发生器
static void Process_Step(float coef)
{
        int tick = 0;
        while (tick < 1000)
        {
                openloop_spd_ref = coef * 1000;
                tick++;
                osDelay(1);
        }
}

// 频率信号发生器
static void Process_Freq(float freq)
{
        int tick = 0;
        float t_ms = round(1000. / freq);
        freq = 1000. / t_ms;
        while (tick < (20 * t_ms))
        {
                openloop_spd_ref = openloop_spd_amplitude * sin( freq * 2 * 3.1415926f * tick * 0.001f);
                tick++;
                osDelay(1);
        }
}

void Test_Response(void)
{
        GimbalYaw_ControlTypeDef *gimbalyaw = GimbalYaw_GetControlPtr();
        #if RESPONSE_MODE == FREQ_RESPONSE
        for (float freq = 1.0f; freq <= 10.0f; freq += 0.5f)
        {
                Process_Freq(freq);
        }
        #endif

        #if RESPONSE_MODE == STEP_RESPONSE
        for (int stepcoef = 1; stepcoef <= 15; stepcoef++)
        {
                Process_Step(stepcoef);
                stepcoef *= -1;
                Process_Step(stepcoef);
        }
        #endif
}

在除云台控制之外的另一个任务中调用 Test_Response()函数，openloop_spd_ref(发给电机的电流)和openloop_spd_fdb(IMU 角速度反馈)为需要采集的数据，

在不同时间段，机器人在架子上不同方位，频率响应和阶跃响应各测四次数据

数据清洗

去除掉频率响应数据中，程序刚运行电机还未启动时的数据

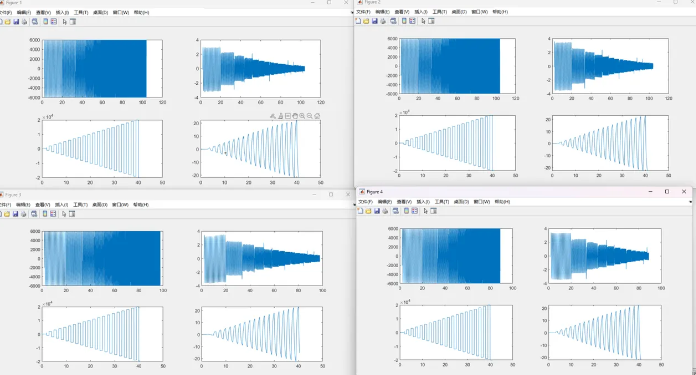
导入 matlab，数据如下：

模型辨识

以频率响应作训练集，阶跃响应作验证集进行线性系统辨识，暂未加入非线性环节，选择传递函数作为系统结构，辨识出的结果如下

选择符合物理规律的电机传递函数$\frac{K}{Ts + 1}$的形式，效果是最好的，置信度在百分之 80 多，如果增加零极点个数，置信度一般在百分之 90 多，但是在验证集上表现会比较差，即出现明显的过拟合

对于系统辨识工具箱中的其它选项，包括拟合算法，频率范围筛选，去除平均值作归一化等预处理和辨识方式，可以根据需要查阅和使用。

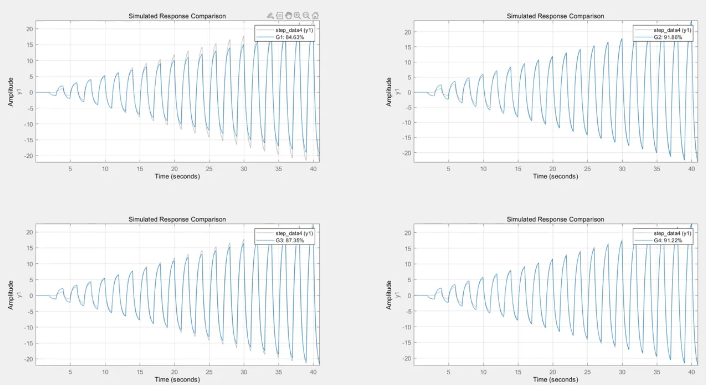
模型验证

阶跃响应作为验证集，效果如下

可以发现，就验证效果而言，相对较好的 G2 和 G4 在幅值变大时效果很好；但所有模型在阶跃响应幅值不大时表现相对交叉，目前怀疑是机器人存在局部非线性环节(如云台松动、静摩擦力等)，在此理想模型的构建中暂时不予考虑。

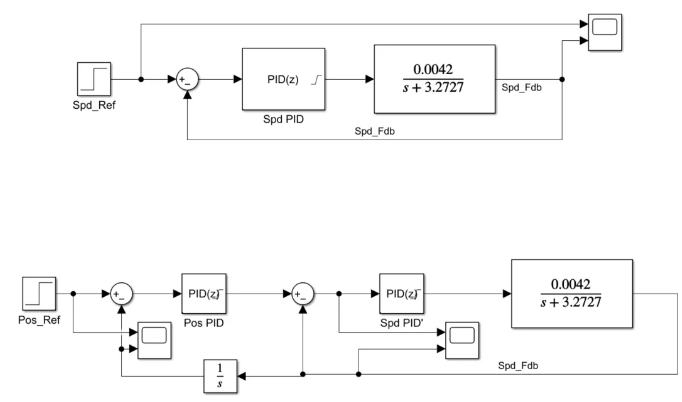
模型仿真与控制器设计

取效果最好的 G2 系统作为云台电机在实际工况下的传递函数，在 simulink 中搭建最简单的速度-角度串级 PID，同时加上输出限幅和积分限幅。使用 PID_Tuner 根据想要的控制效果自动整定，先整定速度环，再整定角度环。

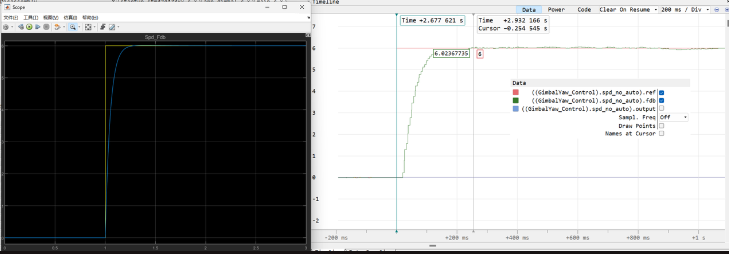
从仿真到实车

将仿真中得到的参数放进代码中运行，得到结果如图，实际结果较好地符合了仿真结果

几点注意：

1. 注意 Matlab 对离散 PID 和滤波器的实现，和代码中是否一致。如步兵老框架中的\(I\)就和离散 PID 算法中的\(I\)不一致，步兵调参中所谓的\(I\)其实是\(I \times \text{d}t\)(采样时间)。
2. 注意检查单位，角度、弧度还是编码器的刻度，建议统一为弧度的标准单位。如步兵老框架中，对 IMU 数据而言，角速度是弧度每秒，角度是度每秒。
3. 就目前(2024.6.21)的效果而言，不敢说实际响应绝对精确地符合仿真，会有那么一点差别。simulink 的 PID 模块内部其实很复杂，以积分抗饱和为例，有 back-calulation 和 clamping 两种实现，笔者尚不清楚它们的实现原理是否跟自己代码中的一致，也有可能导致实际和仿真的误差。但基于辨识整定出的参数一定是能用的，如果发现两者响应大相径庭，建议检查其它问题，如前两条中说的算法实现和单位，以及建模过程的数据采集，模型辨识等。
4. 针对第三点中提到的”实际响应不敢说绝对符合仿真“这一点，一方面是仔细分析，尝试加入非线性环节进行辨识，让模型更逼近实际工况，另一方面，就打比赛而言，笔者更建议是用相对准确的模型自动整定参数，放到机器人上跑，根据实际效果再花个几分钟手动微调达到想要的效果(比如第三点中提到的积分限幅)。