平衡系统建模

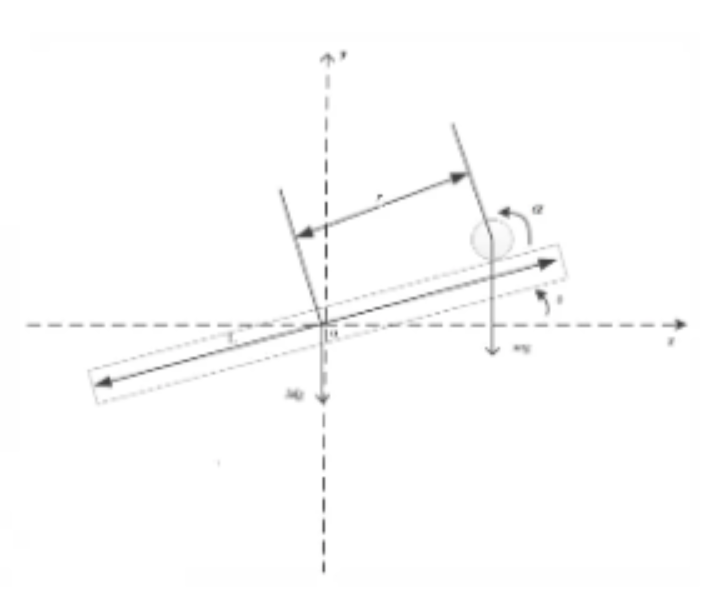
单电机杆球平衡系统建立右图坐标系，符号说明如下：

\(m,M\)分别为球和杆的质量

\(L\)为杆长

\(R\)为球的半径

\(r\)为球到杆中心的位移

\(\theta\)为杆相对于水平方向的夹角

\(\alpha\)为球沿自身轴线旋转的夹角

\(J_L\)为杆绕中心旋转的转动惯量

\(J_b\)为球绕自身轴线旋转的转动惯量

系统动能由球沿杆方向的平动动能、球的自转动能、杆的旋转动能三部分组成

\[\begin{align}&T_1=\frac{1}{2}m[(\dot{x})^2+(\dot{y})^2]=\frac{1}{2}m[(\dot{r})^2+(r\dot{\theta})^2] \\&T_2=\frac{1}{2}J_b\dot{\alpha}^2=\frac{J_b}{2R^2}\dot{r}^2 \\ &T_3=\frac{1}{2}J_L\dot{\theta}^2\end{align}\] \[\begin{align} T &= T_1 + T_2 + T_3 \\ &=\frac{1}{2}m(\dot{r}^2 + r^2\dot{\theta}^2) + \frac{J_b}{2R^2}\dot{r}^2 + \frac{1}{2}J_L \dot{\theta}^2\end{align}\]

系统势能由球的球的重力势能、杆的重力势能两部分组成。其中，由于坐标系原点位于杆中心，故杆的重力势能为 0

\[\begin{align}V = mgr\sin \theta\end{align}\]

拉格朗日量

\[\begin{align}\mathcal{L} &= T - V\\ &=\frac{1}{2}m(\dot{r}^2 + r^2\dot{\theta}^2) + \frac{J_b}{2R^2}\dot{r}^2 + \frac{1}{2}J_L \dot{\theta}^2 - mgr\sin\theta \end{align}\]

由拉格朗日方程

\[\frac{\text{d}}{\text{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}_i}\right) - \frac{\partial \mathcal{L}}{\partial q_i} = Q_i\]

分别以位移\(r\)和夹角\(\theta\)为广义坐标\(q_i\)，得出

\[\begin{align} \left( m + \frac{J_b}{R^2} \right) \ddot{r} + mg\sin\theta - mr\dot{\theta}^2 &= 0 \\ \left( mr^2 + J_L \right) \ddot{\theta} + 2mr\dot{r}\dot{\theta} + mgr\cos\theta &= \tau \end{align}\]

忽略二阶无穷小量\(\dot{\theta}^2\)和\(\dot{r}\dot{\theta}\)，并在平衡点\(\theta = 0\)处作小角度近似，即\(\sin\theta = \theta\)，\(\cos\theta = 1\)，得出

\[\begin{align} \left( m + \frac{J_b}{R^2} \right) \ddot{r} + mg\theta &= 0 \\ \left( mr^2 + J_L \right) \ddot{\theta} + mgr &= \tau \end{align}\]

假设零初始条件，对上述两式作拉普拉斯变换，得出

\[\begin{align} \left(m + \frac{J_b}{R^2}\right) s^2 R(s) + mg\Theta(s) &= 0 \\ \left(mr^2 + J_L\right) s^2 \Theta(s) + mgR(s) &= \tau(s) \end{align}\]

由式\((13)\)得出

\[\begin{align} \frac{R(s)}{\Theta(s)} = -\frac{mg}{\left(m + \frac{J_b}{R^2}\right) s^2} \end{align}\]