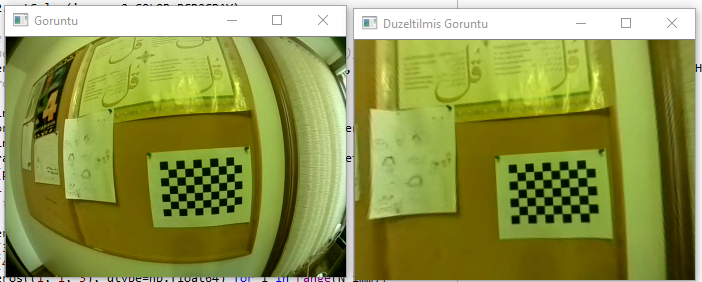
相机模型

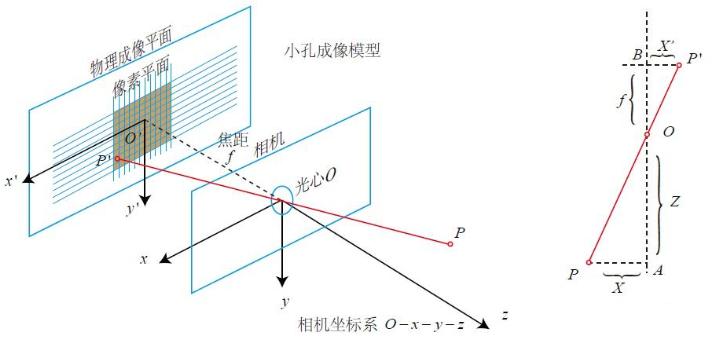
针孔相机模型

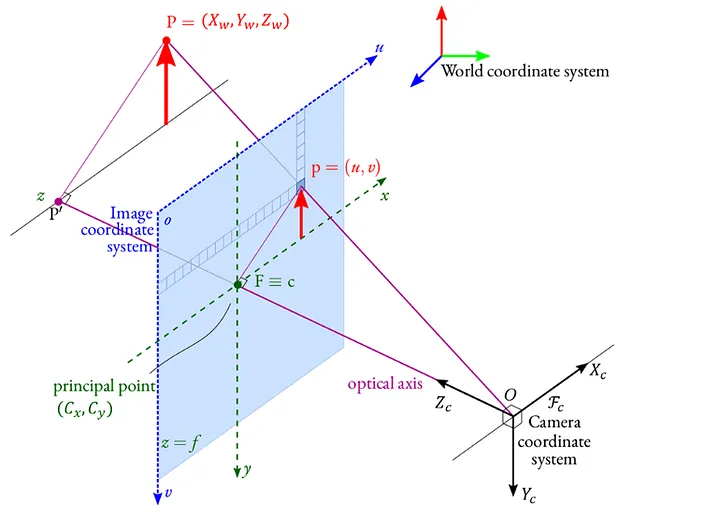
相机模型指三维坐标点到二维成像平面的几何映射关系，具体可以拆解成一系列坐标系之间的转化：世界坐标系–>相机坐标系–>归一化平面坐标系–>图像坐标系。引入归一化平面系的原因一方面是将透视投影的问题建模成归一化的几何问题，另一方面是将畸变建模和标定操作解耦出来在归一化空间中进行。

设世界坐标系中的点为\(\boldsymbol{P}_w\)，相机坐标系中的点为\(\boldsymbol{P}_c\)，归一化平面系中的点为\(\boldsymbol{P}_n\)，图像坐标系中的点为\(\boldsymbol{P}\)

由于世界坐标系固定不变而相机坐标系随机体变化，因此需要通过代表相机位姿的外参矩阵经过刚性变换，从不变的世界坐标系转换到相机坐标系，也叫观测变换

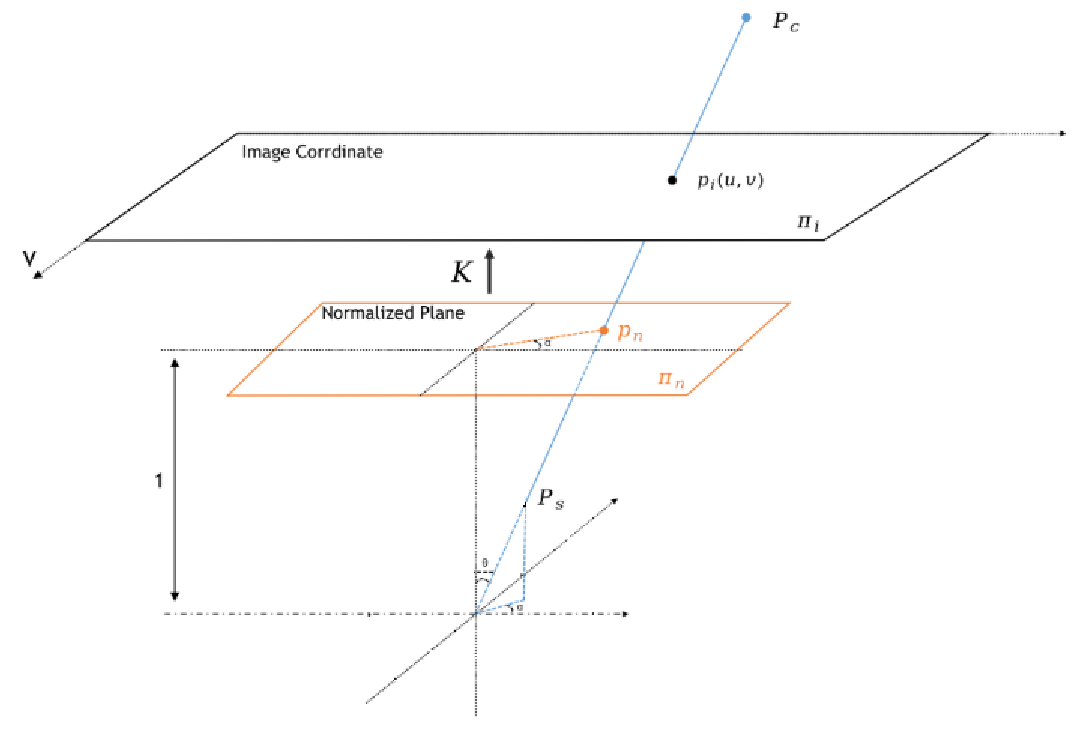
\[\begin{aligned} \boldsymbol{P}_c &= \boldsymbol{T}_{cw}\boldsymbol{P}_w\\ \boldsymbol{T}_{cw} &= [\boldsymbol{R}|\boldsymbol{t}]，为齐次的外参矩阵 \end{aligned}\]

再将相机坐标系中的点缩放到归一化平面坐标系中（也叫透视除法），归一化平面上的点相当于\(\boldsymbol{P}_c\)与光心连线与归一化平面的交点（归一化平面即\(z=1\)平面，即单位焦距的平面）

\[\begin{aligned} \boldsymbol{P}_n = \frac{\boldsymbol{P}_c}{Z_c} &= \left[\frac{X_c}{Z_c}, \frac{Y_c}{Z_c}, 1\right]^\top\\ &= \left[\tan\theta\cos\alpha, \tan\theta\sin\alpha, 1\right]^\top\\ &= \left[u_n, v_n, 1\right]^\top \end{aligned}\]

最后通过相机内参矩阵变换到图像坐标系，也叫透视变换。其中\(f_x、f_y\)分别为两轴焦距，表示一个单位长度对应几个像素；\(c_x、c_y\)为主点偏移，表示光轴在图像中的坐标，在感光元件完全对齐的情况下分别为\(\frac{1}{2}W、\frac{1}{2}H\)

\[\begin{aligned} \begin{bmatrix} u\\ v\\ 1 \end{bmatrix}&= \begin{bmatrix} f_x&0&c_x\\ 0&f_y&c_y\\ 0&0&1 \end{bmatrix} \begin{bmatrix} u_n\\ v_n\\ 1 \end{bmatrix}\\ \boldsymbol{P} &= \boldsymbol{K}\boldsymbol{P}_n，\boldsymbol{K}为内参矩阵 \end{aligned}\]

三个步骤的操作合在一起称为投影矩阵。

全向模型

相机根据视场角（Field Of Vision）的大小分为：普通相机（FOV 小于 90 度）、广角相机（FOV 大于 90 度，小于 180 度）和全向相机（FOV 大于 180 度）。由于不可能通过透视投影将半球形视野投影到有限的图像平面上，因此为广角/鱼眼/全向相机引入了归一化球面坐标系。

设归一化球面系中的点为\(\boldsymbol{P}_s\)，光线与主光轴夹角为\(\theta\)，光线在投影平面上与水平方向夹角为\(\alpha\)，光线在投影平面上长度为\(\rho\)

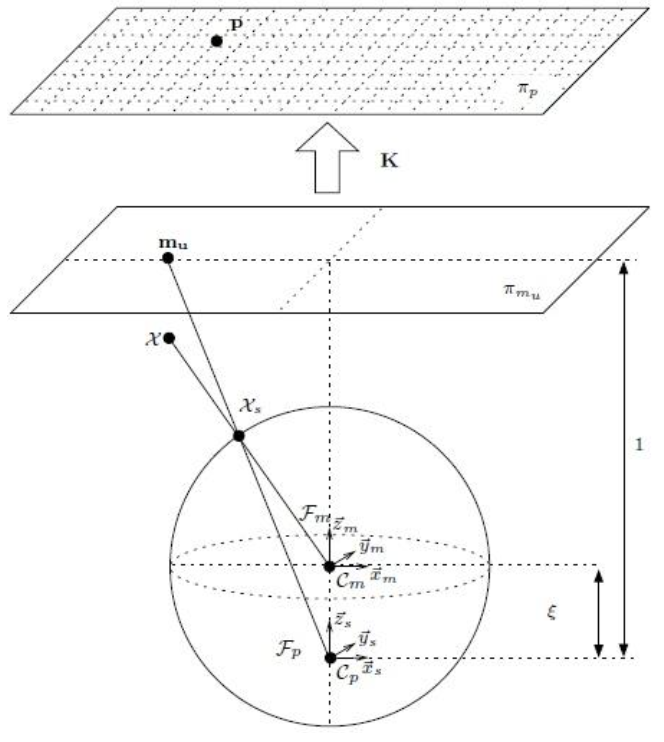\(\begin{aligned} \boldsymbol{P}_s &= \frac{\boldsymbol{P}_c}{||\boldsymbol{P}_c||} = \left[\frac{X_c}{||\boldsymbol{P}_c||}, \frac{Y_c}{||\boldsymbol{P}_c||}, \frac{Z_c}{||\boldsymbol{P}_c||}\right]^\top\\ \theta &= \arctan \frac{\rho}{Z_s} = \arcsin \frac{\rho}{1}\\ \alpha &= \arctan \frac{Y_s}{X_s}\\ \rho &= \sqrt{X_s^2 + Y_s^2} \end{aligned}\) 缩放到单位球面后，将坐标系向下平移\(\xi\)的距离，再转化到归一化平面上，后续步骤同针孔相机模型（此处以CMei模型为例，实际上还有KannalaBrandt模型）。

畸变模型

实际使用中，会在感光元件和被观测物体之间加入透镜并引入畸变，畸变指相机成像过程与针孔模型的差异。只对图像造成半径方向上的伸缩变化的称为径向畸变，由透镜本身形状引起，又分桶形畸变和枕形畸变；对图像造成平移的称为切向畸变，由镜头加工误差和安装误差导致透镜和成像平面并不完全平行引起。

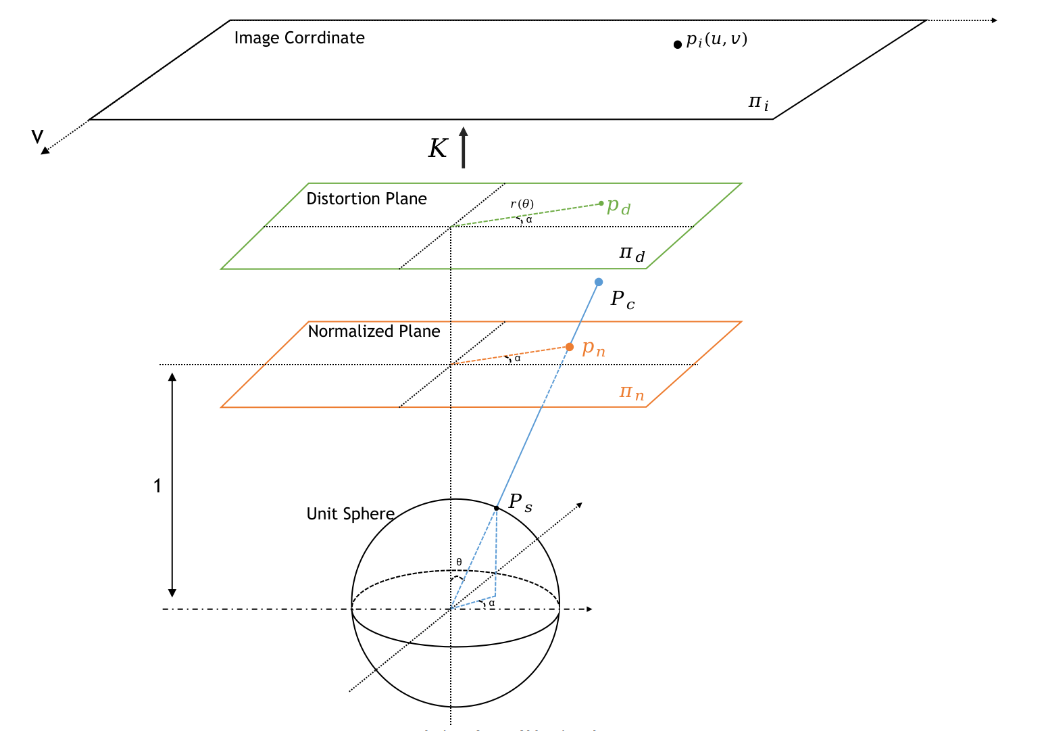
为了建模畸变，在归一化平面的位置引入畸变平面（仍然\(z=1\)，图中将它们错开了，实际上与归一化平面处于同一位置）。在畸变平面中，用具有一般性的多项式函数来表达不同畸变的投影模型。

设畸变平面上的点为\(\boldsymbol{P}_d = [u_d, v_d, 1]^\top\)，归一化平面中的点为\(\boldsymbol{P}_n = [u_n, v_n, 1]^\top\)，到归一化平面原点的距离为\(r = \sqrt{u_n^2 + v_n^2}\)。畸变可表达如下，其中\(k_1、k_2、k_3、p_1、p_2\)为畸变参数，可通过标定求得。

\[\begin{aligned} &\begin{cases} u' = u_n(1 + k_1 r^2 + k_2 r^4 + k_3 r^6) \\ v' = v_n(1 + k_1 r^2 + k_2 r^4 + k_3 r^6) \end{cases}\quad &径向畸变\\ &\begin{cases} u_d = u' + 2 p_1 u_n v_n + p_2 (r^2 + 2 u_n^2) \\ v_d = v' + p_1 (r^2 + 2 v_n^2) + 2 p_2 u_n v_n \end{cases}\quad &切向畸变\\ \end{aligned}\]

所谓的去畸变，就是将图像经透视反变换到畸变平面上，进行反畸变，在透视投影回图像平面的过程，这样就可以得到符合针孔投影模型规律的无畸变图像。