空间位姿表示
用于表示空间位姿的数学工具
Rodrigue 旋转公式
在三维空间中，给定旋转轴和旋转角度可由Rodrigue（罗德里格） 旋转公式得到旋转后的结果以及旋转矩阵，其中\(\boldsymbol{k}\)为旋转轴方向的单位向量，\(\theta\)为要旋转的角度，\(\boldsymbol{v}\)被旋转的向量，\(\boldsymbol{v}_\text{rot}\)为旋转后的向量，\(\boldsymbol{R}\)为提取出的旋转矩阵
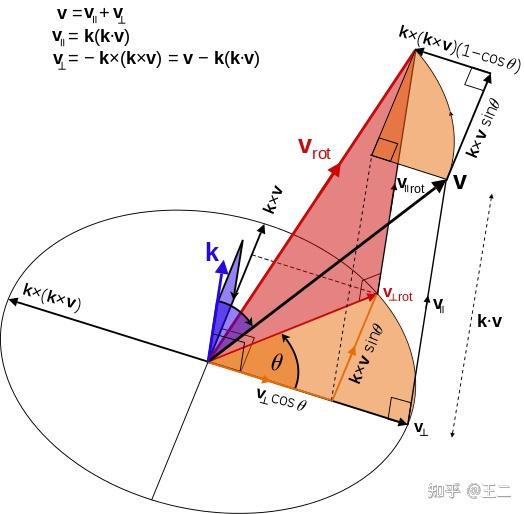\(\begin{aligned} \boldsymbol{v}_{\text{rot}} &= \boldsymbol{v} \cos \theta + (\boldsymbol{k} \times \boldsymbol{v}) \sin \theta + \boldsymbol{k} (\boldsymbol{k} \cdot \boldsymbol{v})(1 - \cos \theta)\\ &= \boldsymbol{R} \boldsymbol{v}\\ \boldsymbol{R} &= \boldsymbol{I} + \sin\theta \, [\boldsymbol{k}]_\times + (1 - \cos\theta) \, [\boldsymbol{k}]_\times^2 \end{aligned}\) \([\boldsymbol{k}]_\times\)为\(\boldsymbol{k}\)对应的叉乘矩阵，是用于描述向量叉乘的矩阵形式，\(\boldsymbol{k} \times \boldsymbol{x} = [\boldsymbol{k}]_\times \cdot \boldsymbol{x}\) \(\begin{aligned} [\boldsymbol{k}][\boldsymbol{k}]_\times &= \begin{bmatrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x & 0 \end{bmatrix}\\ \end{aligned}\) 二维下旋转矩阵简化如下，其中\([1]_\times=\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}\)，表示旋转90°的旋转矩阵，作用相当于虚数单位\(\text{i}\) \(\begin{aligned} \boldsymbol{R} &= \boldsymbol{I} \cos\theta + [1]_\times \sin\theta \\ &= \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \end{aligned}\)
李群和李代数
李群是抽象的，可以作为对其它集合中元素进行的一种操作，包括取逆、插值、刚体变换、进行微积分等。平面中的刚体运动可以用\(SE(2)\)表示，空间中的刚体运动可以用\(SE(3)\)表示。李群一方面是一个群，另一方面也是一个光滑的流形。
切空间是线性的向量空间，在切空间中可以进行微积分运算。在单位点出的切空间称为李代数。把切空间映射到流形上的操作称为指数映射，反之将流形映射到切空间上则为对数映射。由于李群是光滑的流形，因此每个点出有唯一的切空间。
李群中的运算如下 \(\begin{aligned} \mathcal{X}\oplus\omega&\triangleq\mathcal{X}\cdot\text{Exp}(\omega)\\ \mathcal{Y}\ominus\mathcal{X}&\triangleq\text{Log}(\mathcal{X}^{-1}\cdot\mathcal{Y}) \end{aligned}\)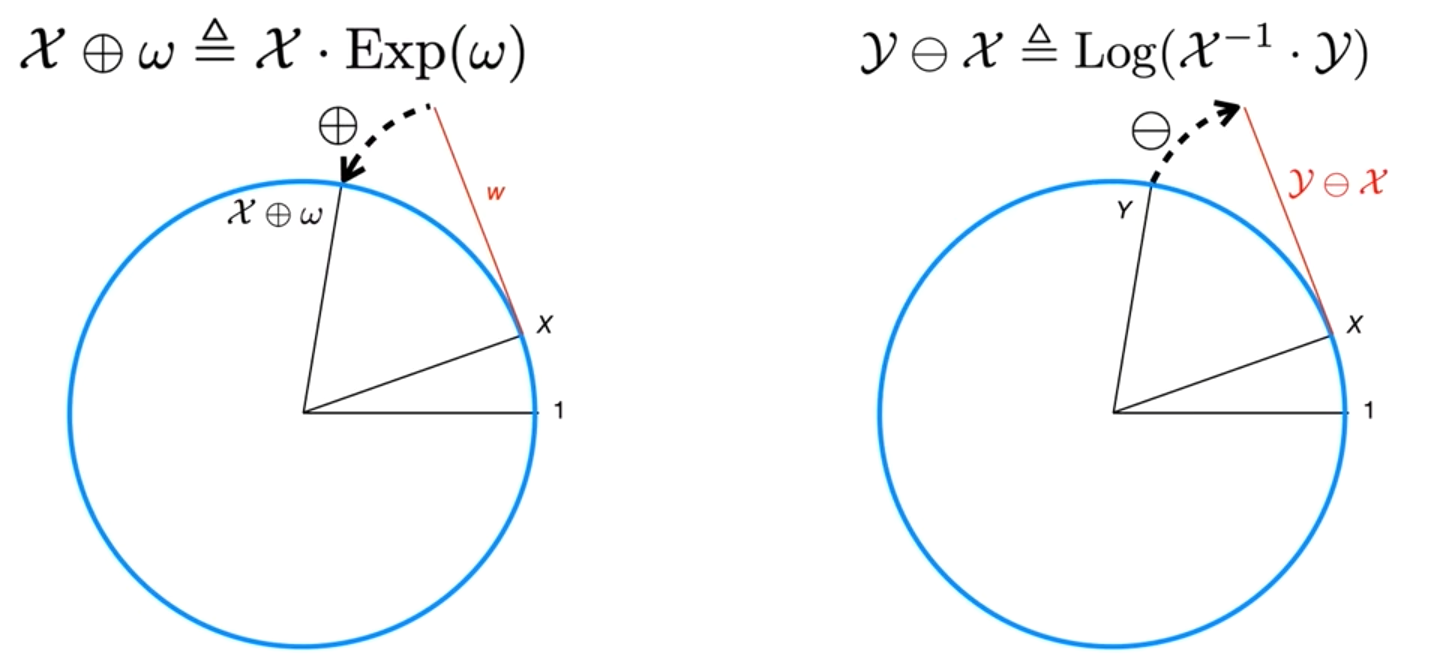 
雅可比矩阵定义如下 $$ \begin{aligned}
\mathbf{J}&=\frac{Df(\mathcal{X})}{D\mathcal{X}}=\lim_{\boldsymbol{\tau}\to 0}\frac{f(\mathcal{X}\oplus\boldsymbol{\tau})\ominus f(\mathcal{X})}{\boldsymbol{\tau}}\in\mathbb{R}^{n\times m} \end{aligned} $$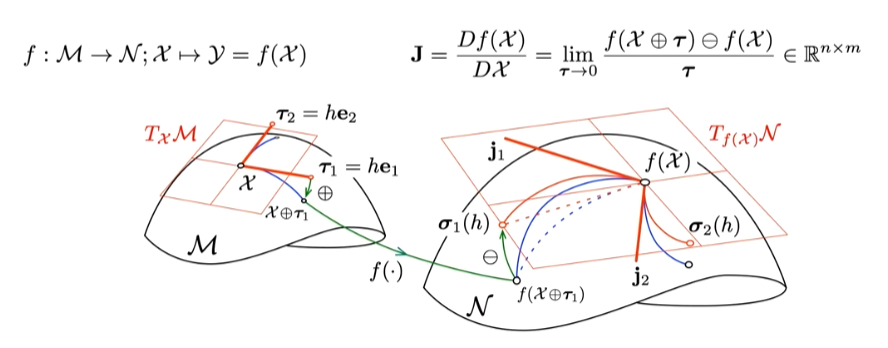 
例如，对\(SO(3)\)中的旋转操作求导 \(f:SO(3)\times\mathbb{R}^3\to\mathbb{R}^3\quad ;\quad (\mathbf{R},\mathbf{p})\mapsto f(\mathbf{R},\mathbf{p})=\mathbf{R}\cdot\mathbf{p}\\\) 分别对\(\boldsymbol{R}\)和\(\boldsymbol{p}\)求导 \(\begin{aligned} \frac{Df}{D\mathbf{R}}&=\lim_{\boldsymbol{\theta}\to 0}\frac{(\mathbf{R}\oplus\boldsymbol{\theta})\cdot\mathbf{p}-\mathbf{R}\cdot\mathbf{p}}{\boldsymbol{\theta}}\\ &=\lim_{\boldsymbol{\theta}\to 0}\frac{(\mathbf{R}\cdot\text{Exp}(\boldsymbol{\theta}))\cdot\mathbf{p}-\mathbf{R}\cdot\mathbf{p}}{\boldsymbol{\theta}}\\ &=\lim_{\boldsymbol{\theta}\to 0}\frac{\mathbf{R}\cdot(\mathbf{I}+\boldsymbol{\theta}_\times)\cdot\mathbf{p}-\mathbf{R}\cdot\mathbf{p}}{\boldsymbol{\theta}}\\ &=\lim_{\boldsymbol{\theta}\to 0}\frac{\mathbf{R}\cdot\boldsymbol{\theta}_\times\cdot\mathbf{p}}{\boldsymbol{\theta}}\\ &=\lim_{\boldsymbol{\theta}\to 0}\frac{-\mathbf{R}\cdot\mathbf{p}_\times\cdot\boldsymbol{\theta}}{\boldsymbol{\theta}}\\ &=-\mathbf{R}\cdot\mathbf{p}_\times\\ \frac{Df}{D\mathbf{p}}&=\lim_{\delta\mathbf{p}\to 0}\frac{\mathbf{R}\cdot(\mathbf{p}+\delta\mathbf{p})-\mathbf{R}\cdot\mathbf{p}}{\delta\mathbf{p}}\\ &=\lim_{\delta\mathbf{p}\to 0}\frac{\mathbf{R}\cdot\delta\mathbf{p}}{\delta\mathbf{p}}=\mathbf{R} \end{aligned}\)