高斯泼溅

高斯泼溅原理与实现

发表于 2025/08/22 更新于 2025/10/08

高斯泼溅

作者 Hatrix

72 分钟阅读

高斯泼溅

概览

高斯泼溅是基于 Splatting 和机器学习的三维重建方法。根据多视角图像，从 SfM 生成的点云和相机参数矩阵出发，将点膨胀成带有位置、形状、颜色和不透明度参数的高斯椭球，并以此为基本单位来表示场景。为了实现对三维场景的高质量表达，高斯泼溅通过深度学习的方式优化高斯椭球的参数。具体来说，是将用高斯椭球表示的三维场景按照给定的视角投影到二维平面得到渲染图像，渲染图像与真值图像作 loss，反向传播到各个可学习参数上完成优化。整个流程归纳为下图，本文也会围绕此图，记录其中的原理和实现细节。(注，本文提到的高斯泼溅，均指在 SIGGRAPH 2023 上发表的原版 3DGS，以下统称高斯泼溅)

SfM

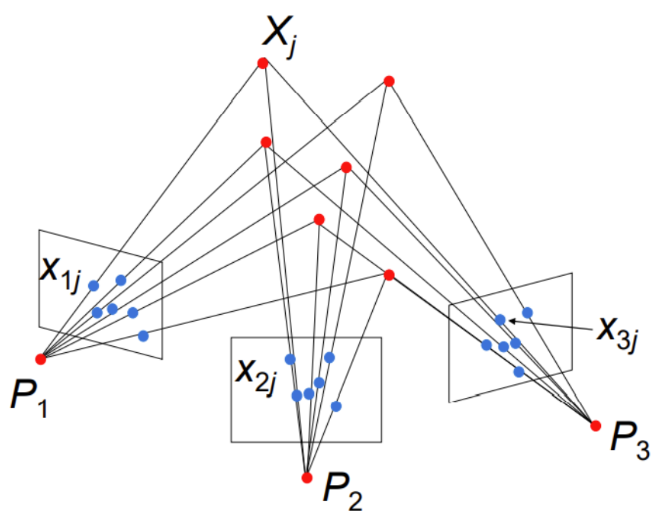
从多视角图像生成三维点云的方法主要分为 SfM + MVS 的几何方法和基于 VGGT 架构的 transformer 方法，高斯泼溅用到的是几何方法中 SfM 生成的稀疏点云和相机参数。SfM(Structure from Motion，运动恢复结构)是一种从多视角图像中恢复三维结构和相机运动的计算机视觉技术，通过特征点匹配和对极约束的纯几何方法，估计每张图像对应的相机位姿和各个特征点在三维中的位置，并进行全局的多视图几何优化，最终得到稀疏点云和相机的内外参。

SfM 并不是高斯泼溅中研究的内容，高斯泼溅中直接使用 COLMAP 这个 SfM 工具，调用 COLMAP 的命令完成特征提取、特征匹配、稀疏重建和图像去畸变四个步骤，获得场景的稀疏点云和相机内外参。对 COLMAP 工具提供的读取函数进行重构，并根据后续算法需要，将需要的数据加工组织如下：

Intrinsics：焦距在两轴方向像素坐标下的表示、两轴主点偏移、图像的宽度和高度
Extrinsics：旋转四元数、平移向量
Viewpoints：两轴向的视场角、世界坐标系到相机坐标系的转换矩阵(numpy array 和 torch tensor)、投影矩阵(torch tensor)、变换矩阵(torch tensor)、相机位置(torch tensor)
ImageInfos：图像文件名、图像宽度和高度、图像本身(PIL image 和 torch tensor)
SceneInfo：稀疏点云的位置和颜色、所有相机位置的中心到最远相机的距离

相机模型

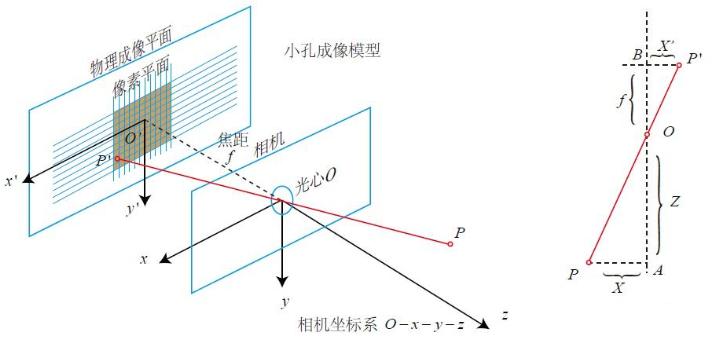
相机模型是计算机视觉中描述物理相机成型过程的数学模型，用于建立三维坐标点到二维成像平面的几何映射关系；将这个映射过程中涉及的参数提取出来代表相机在成像中的作用，就是相机模型。相机模型中的参数分为内参和外参，为了使用线性代数的工具完成映射过程中的坐标变换，将参数组织成矩阵的形式，即内参矩阵和外参矩阵。

不同种类相机的内参数量和形式是不同的，最简单的针孔相机内参包含两个轴向的焦距和主点偏移。除了针孔相机，其它相机模型如鱼眼相机、全向相机的内参还有各种畸变参数等。高斯泼溅中使用的相机模型为针孔相机，故本文也以针孔相机为前提介绍后续内容。

\[\begin{aligned} 内参矩阵: \mathbf{K}= \begin{bmatrix} f_x&0&c_x\\ 0&f_y&c_y\\ 0&0&1 \end{bmatrix} \end{aligned}\]

几何光学中的物理焦距是光心到图像平面的距离，相机的镜头一般认为是各向同性的，成像平面也只有一个，因此物理焦距\(f\)是唯一的，这里的\(f_x\)和\(f_y\)是指焦距在像素坐标系下的表示，它们与\(f\)的关系如下式，其中\(s_x\)和\(s_y\)分别表示像素在 x 和 y 方向上的物理尺寸，由于制造工艺的缺陷，像素可能并不是标准的正方形，因此\(s_x\)可能并不等于\(s_y\)，也就产生了所谓的\(f_x\)和\(f_y\)。计算机视觉中的焦距一般指这个像素坐标系下的表示，即\(f_x\)和\(f_y\)(代码中命名为 focal x 和 focal y)，而非几何光学中的物理焦距\(f\)。

\[\begin{aligned} f_x = \frac{f}{s_x}\\ f_y = \frac{f}{s_y}\\ \end{aligned}\]

由两轴焦距和图像的宽度和高度，可以计算得出两个方向上的视场角(field of view，简称 fov)；视场角定义为相机在某一方向上可见的角度范围

\[\begin{aligned} \text{fovx} = 2\arctan\frac{\text{width}}{2 f_x}\\ \text{fovy} = 2\arctan\frac{\text{height}}{2 f_y}\\ \end{aligned}\]

主点偏移是光轴投影到像素坐标系中的坐标。光轴投影(忽略深度)的结果是图像坐标系中的表示，图像坐标系的原点在图像正中心，而像素坐标系的原点在图像的最左上角，即左上角像素的左上角，因此两个二维坐标系之间有一个\((\frac{w}{2}, \frac{h}{2})\)的偏移(w 和 h 分别表示图像的宽度和高度)，这就是所谓的主点偏移。

外参具有统一的形式，即相机的位置和姿态。

\[\begin{aligned} 外参矩阵&: \mathbf{T}= \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0} & 1 \end{bmatrix}= \begin{bmatrix} \mathbf{I} & \mathbf{t} \\ \mathbf{0} & 1 \end{bmatrix} \times \begin{bmatrix} \mathbf{R} & \mathbf{0} \\ \mathbf{0} & 1 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} r_{xx} & r_{xy} & r_{xz} & 0 \\ r_{yx} & r_{yy} & r_{yz} & 0 \\ r_{zx} & r_{zy} & r_{zz} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\\ \end{aligned}\]

整个成像的过程可以拆解成一系列坐标系之间的转化：世界坐标系–>相机坐标系–>归一化设备坐标系–>像素坐标系。

图形学基础

视锥

视锥(view frustum)是计算机图形学中用于描述虚拟相机的可见区域的几何体，只有在视锥中的点才可能被投影到图像平面上(这里隐含了裁剪的操作，即只有视锥内的部分才会参与后续的渲染)；视锥定义为一个截头的四棱锥体，锥的顶点为相机光心，由近平面和远平面两个平行平面截切四棱锥体，得到的四棱台就称为视锥。

视锥包含的范围由近平面和远平面深度(znear 和 zfar)以及两轴的视场角确定，其中近平面和远平面分别界定了虚拟相机最近和最远的可见深度。高斯泼溅中相机坐标系为右手系，即以相机光心为原点，向右为 x 轴方向，向上为 y 轴方向，向前为-z 轴方向建立坐标系，再假设近平面矩形上下边的 y 值和左右的 x 值分别设为\(t、b、l、r\)(top、bottom、left、right)，有如下计算关系

\[\begin{aligned} t &= \tan\frac{\text{fovy}}{2} \cdot \text{znear}\\ b &= -t = -\tan\frac{\text{fovy}}{2} \cdot \text{znear}\\ r &= \tan\frac{\text{fovx}}{2} \cdot \text{znear}\\ l &= -r = -\tan\frac{\text{fovx}}{2} \cdot \text{znear}\\ \end{aligned}\]

仿射变换

仿射变换是将一个向量空间进行一次线性变换加一次平移变换(这里的线性变换指线性代数定义上的线性变换，即满足对加和数乘封闭的变换)，从而变换到另一个向量空间的操作。仿射变换具有一定的保持性：变换前后点还是点、线还是线、面还是面；平行线和平行面依然平行；图形间的比例关系不变。仿射变换包含的操作类型有伸缩、旋转、剪切、镜像和平移；其中平移通过向量加法实现，另外四种操作通过矩阵乘法实现。

设原始图像中的坐标为\((u, v)\)，变换后图像坐标为\((x, y)\)；将坐标表示为行向量，对行向量应用变换使用矩阵右乘。(注：在 numpy 这样具有向量化的乘法矩阵算子库中，使用行向量表示坐标以及相应地使用右乘矩阵，可以不必再对坐标矩阵调整通道并 reshape，因此一些资料中会使用行向量来表示坐标。)仿射变换通式用矩阵表达如下，将\((u, v)\)表示为\([u, v, 1]\)是为了将平移操作统一纳入矩阵乘法减少运算次数，从而用一次矩阵乘法实现仿射变换通式；有时也会将变换矩阵凑成方阵而将\((x, y)\)也表示为齐次坐标。通过多组点求解超定方程组的最小二乘解即可得出仿射变换矩阵(求解过程可见参考资料)。

\[\begin{aligned} &\begin{bmatrix} x & y \end{bmatrix} = \begin{bmatrix} u & v & 1 \end{bmatrix} \begin{bmatrix} t_{11} & t_{12} \\ t_{21} & t_{22} \\ t_{31} & t_{32} \end{bmatrix} \\ &\begin{bmatrix} x & y & 1 \end{bmatrix} = \begin{bmatrix} u & v & 1 \end{bmatrix} \begin{bmatrix} t_{11} & t_{12} & 0 \\ t_{21} & t_{22} & 0 \\ t_{31} & t_{32} & 1 \end{bmatrix} \end{aligned}\]

透视投影

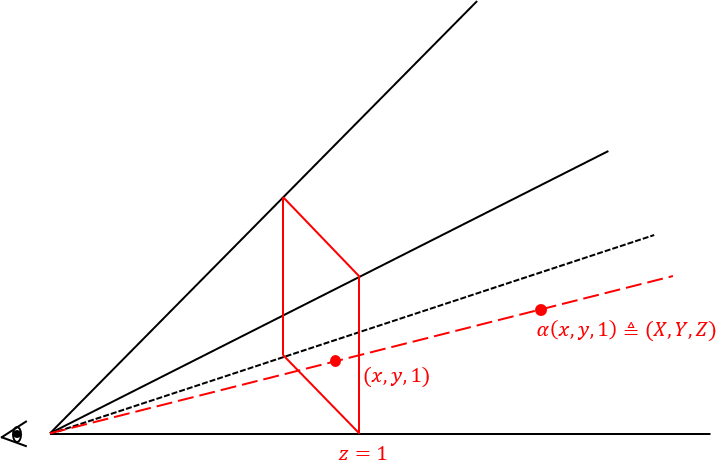
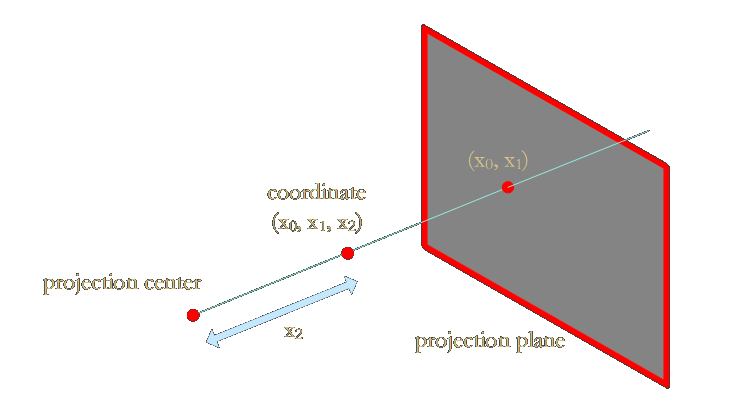
计算机图形学中的投影分为正交投影和透视投影，人眼和相机成像的规律都符合透视投影，以下的介绍也针对透视投影。用相机进行拍摄时，认为三维空间中的物体都投影在一个二维平面上，如下图中的红色平面。将这个平面定义为\(z=1\)的平面，称为归一化投影平面。设\((x, y, 1)\)为二维图像上点\((x, y)\)在三维的坐标。对这个三维坐标乘以系数\(\alpha\)，令\((X, Y, Z) = \alpha (x, y, 1)\)，\(\alpha\)改变的过程，就是点在红色虚线上移动的过程。

对于归一化投影平面而言，所谓的透视投影，就是将点从\((X, Y, Z)\)变换到\((x,y, 1)\)的过程。显然，对点\((X, Y, Z)\)除以\(Z\)分量就可以得到在归一化投影平面上的坐标\((x, y)\)，即\((x, y) = (\frac{X}{Z}, \frac{Y}{Z})\)。设原始图像中的坐标为\((u, v)\)，变换后图像坐标为\((x, y)\)；由于投影是空间中的变换，因此将原始图像上的点表示为齐次坐标\((u, v, w)\)，透视投影变换通式用矩阵表达如下。与仿射变化矩阵类似，通过多组点求解超定方程组的最小二乘解即可得出透视投影变换矩阵(求解过程可见参考资料)。

\[\begin{aligned} \begin{bmatrix} x & y & 1 \end{bmatrix} = \begin{bmatrix} u & v & w \end{bmatrix} \begin{bmatrix} t_{11} & t_{12} & t_{13} \\ t_{21} & t_{22} & t_{23} \\ t_{31} & t_{32} & 1 \\ \end{bmatrix} \end{aligned}\]

真实相机的成像平面可能不是归一化投影平面，透视投影需要由齐次坐标通过内参矩阵计算，得到像素平面上的坐标为

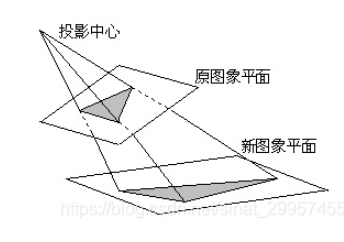
\[\begin{aligned} x = f_x\frac{u}{w} + c_x\\ y = f_y\frac{v}{w} + c_y\\ \end{aligned}\]

无论是哪种，透视投影含有对\(Z\)的除法，因此是非线性变换。总体而言，透视投影是将图片通过投影矩阵投影到新的视平面的过程。矩形经过透视投影之后可能变成任意四边形，但直线仍然保持为直线。

足迹渲染

足迹渲染(footprint)的概念源于纹理映射，即像素平面和纹理空间的对应关系，通俗理解就是给纯色的几何体上贴图的过程。由于此处并不研究纹理相关的内容，故不作过多介绍。高斯泼溅在渲染过程中用到的渲染足迹概念，来自 EWA Volume Splatting，是指三维体素投影到二维平面上对应的这块区域。为了进一步介绍，还需要明确一些前置概念。

kernel 定义为一个局部加权函数，用于决定邻域的贡献大小，简单来说就是影响范围+权重函数。体素在三维空间中就是一个 3D kernel，投影到屏幕空间后得到的 footprint 就是一个 2D kernel，投影变换直接决定了 footprint 的形状。

EWA filtering 指出，纹理映射时存在固有的混叠问题，一个屏幕像素可能覆盖纹理空间中的多个纹理像素，如果只使用最近点采样或双线性插值，会出现锯齿、闪烁或马赛克等视觉伪影。抗混叠的关键是对这片纹理区域做平均而不是对单个点采样。这个区域的形状一般是一个平行四边形，经过近似后用一个椭圆来表示。在椭圆范围内使用高斯滤波在椭圆内进行平滑采样，即对纹理做加权平均，从而避免混叠。之所以用椭圆来近似是由于抗混叠的采样需要平滑的低通滤波，而平行四边形的硬边界会引入额外的频率成分。

EWA Volume Splatting 中沿用了这一思想并将其推广到体素中，由于任意体素投影得到的 footprint 形状复杂，直接处理的计算开销较大；且出于上述抗混叠的考虑，用椭圆 kernel 来近似投影得到的 footprint，衡量三维 kernel 对图像平面上每个点的贡献。而高斯泼溅沿用了 EWA Volume Splatting 的方法，同样用椭圆表示 footprint。

高斯椭球

对于 SfM 获得的点云，用三维的高斯函数(kernel)将它们膨胀成带有位置、形状、颜色和不透明度的椭球。这个所谓的膨胀，其实是用 KNN 取最近邻三个点的平均半径作为初始化高斯椭球的主轴长度，并以点的颜色作为椭球的初始颜色。

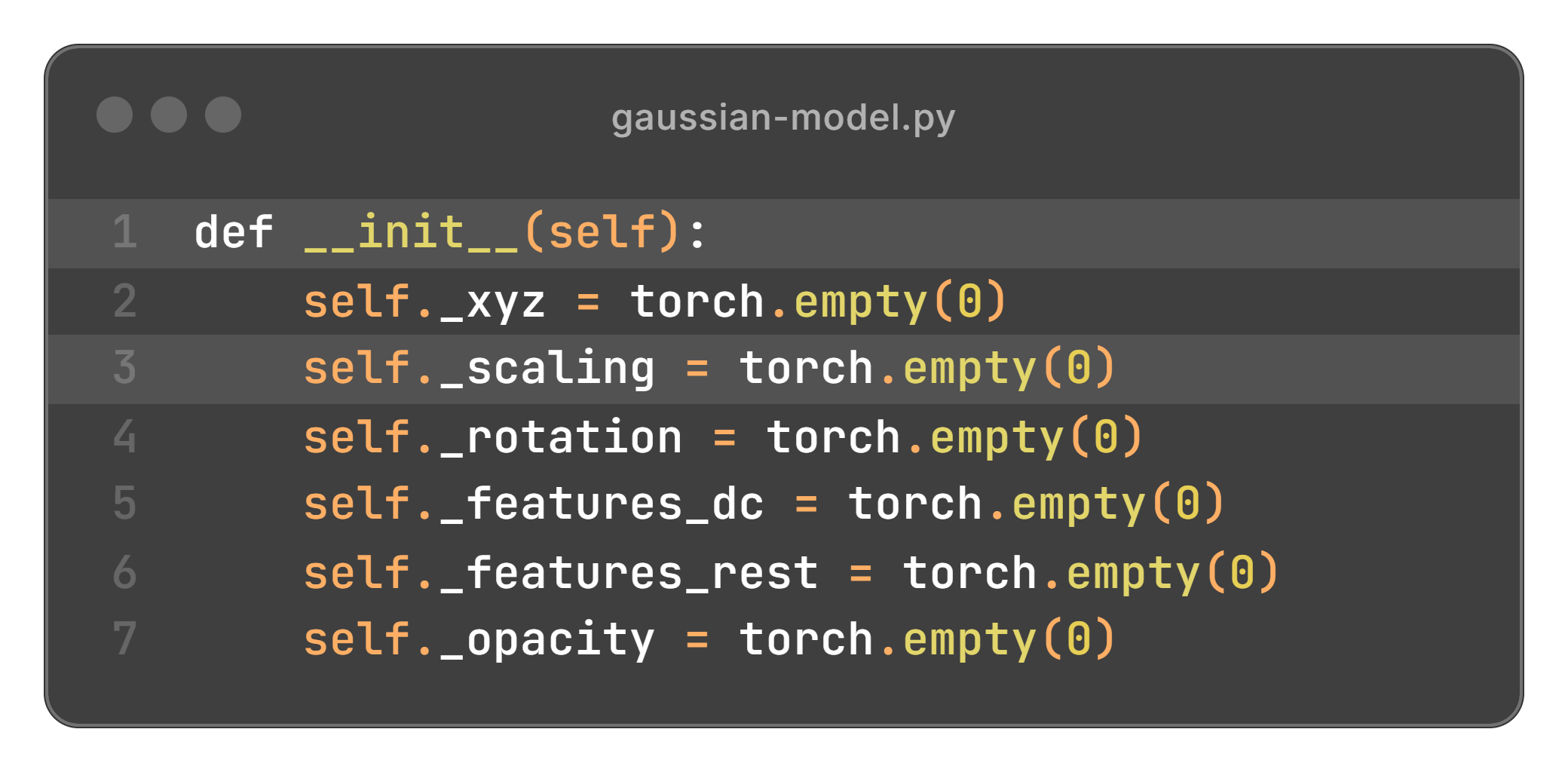
这些参数都是可学习的，会在后续的流程中以深度学习的方法进行优化，且为了保证这些参数的取值符合自身的物理意义(主轴长度为正、旋转矩阵为正交矩阵、协方差矩阵为半正定对称矩阵、不透明度在 0-1 之间)，会将这些参数通过所谓的激活函数之后再使用。高斯椭球的参数在程序中组织如下，其中 xyz 为位置、scaling 和 roration 为控制形状的主轴长度和旋转四元数、features dc 和 features rest 分别为球谐系数的直流分量(0 次球谐系数)和剩余分量(其它阶次球谐系数)、opacity 为不透明度。

之所以选择高斯椭球作为场景的表达基元而不是立方体或其它形式，是因为高斯函数具有良好的数学性质，一是高斯函数对仿射变换封闭(渲染中需要用到仿射变换)，二是高斯函数可微，且三维高斯沿某一个轴积分成二维后仍为高斯函数(渲染实质上就是投影到二维平面)，三是高斯椭球本身是各向异性的体素，比各向同性的高斯球表现力更强。

位置和形状

这个所谓的椭球形状，是由高斯函数的数学表达式决定的(高维高斯均假设各向异性，即不同方向梯度不同)

\[\begin{aligned} G(x) &= \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(x - \mu)^2}{2\sigma^2} \right)\\ G(\mathbf{x}) &= \frac{1}{2\pi \sqrt{|\mathbf{\Sigma}|}} \exp\left( -\frac{1}{2} (\mathbf{x} - \mathbf{\mu})^\top \mathbf{\Sigma}^{-1} (\mathbf{x} - \mathbf{\mu}) \right),\\ &\text{其中 } \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix},\quad \mathbf{\mu} = \begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix},\quad \mathbf{\Sigma} = \begin{bmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{bmatrix}\\ G(\mathbf{x}) &= \frac{1}{(2\pi)^{3/2} \sqrt{|\mathbf{\Sigma}|}} \exp\left( -\frac{1}{2} (\mathbf{x} - \mathbf{\mu})^\top \mathbf{\Sigma}^{-1} (\mathbf{x} - \mathbf{\mu}) \right),\\ &\text{其中 } \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix},\quad \mathbf{\mu} = \begin{bmatrix} \mu_1 \\ \mu_2 \\ \mu_3 \end{bmatrix},\quad \mathbf{\Sigma} = \begin{bmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{bmatrix}\\ \mathbf{\mu}为均值&，决定分布的位置\\ \mathbf{\Sigma}为协方&差矩阵，为半正定的对称矩阵，对角线元素为方差，其余元素为协方差，决定分布的形状 \end{aligned}\]

先以二维为例，令二维高斯函数为某一常数，提取各高次项系数并整理之后可以得到一个标准的椭圆方程；这一点从几何意义上理解更直观：想象一个平面与钟形曲面相交，截出的曲线就是椭圆。三维高斯函数同理，令其为常数并提取各高次项系数，整理之后就是一个标准的椭球面方程。在几何意义上为了可视化出来，可以想象用颜色而非欧式距离来代表函数值，这样，三维高斯函数就是一个实心椭球，从内到外就是颜色渐变的椭球壳。

高斯椭球的位置和形状分别由三维高斯分布中的均值和协方差矩阵确定，均值确定位置很好理解，下面解释协方差如何确定形状。

任意高斯分布可由标准高斯分布通过仿射变换得到，对高斯函数进行仿射变换满足如下规律(推导过程可见 EWA Volume Splatting，简单来说就是写出高斯函数的表达式，应用仿射变换代入并加以整理便可得到这个规律)

\[\begin{aligned} \mathbf{x} &\sim \mathcal{N}(\mathbf{\mu}, \mathbf{\Sigma})\\ \mathbf{y} &= \mathbf{A} \mathbf{x} + \mathbf{b}\\ \mathbf{y} &\sim \mathcal{N}(\mathbf{A} \mathbf{\mu} + \mathbf{b},\ \mathbf{A} \mathbf{\Sigma} \mathbf{A}^\top)\\ \end{aligned}\]

由于仿射变换本身可以表达为旋转、缩放和平移(\(\mathbf{A} \mathbf{x} + \mathbf{b} = \mathbf{R}\mathbf{S} \mathbf{x} + \mathbf{b}\))的组合。标准正态分布的协方差矩阵\(\mathbf{\Sigma}=\mathbf{I}\)，因此变换之后的协方差矩阵\(\mathbf{\Sigma’}\)可以写成下式，即用旋转矩阵和缩放矩阵构成协方差矩阵。

\[\mathbf{\Sigma’} = \mathbf{A}\mathbf{I}\mathbf{A}^\top = \mathbf{R}\mathbf{S}\mathbf{S}^\top\mathbf{R}^\top\]

之所以要这样分解，是为了在参数学习的过程中自然地满足协方差矩阵为半正定的对称矩阵这一约束(旋转矩阵为正交矩阵，满足转置等于逆的性质，而缩放矩阵为对角矩阵，两者合成为\(\mathbf{R}~ \text{diag}(\sigma_1^2 \, \sigma_2^2 \, \sigma_3^2) ~\mathbf{R}^\top\)，满足半正定对称矩阵的要求)。旋转矩阵控制了椭球绕三个坐标轴的旋转角度，缩放矩阵控制了椭球三个主轴的长度，因此它们构成的协方差矩阵决定了椭球的形状。(注：这一点如果从代数上理解，其实就是协方差矩阵的二次型对应的几何图像，即椭圆。协方差矩阵中的方差项和协方差项就分别控制着椭圆的长轴长度和绕坐标轴的旋转角度)

颜色

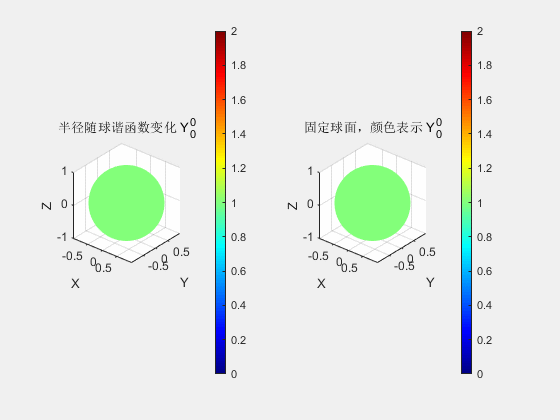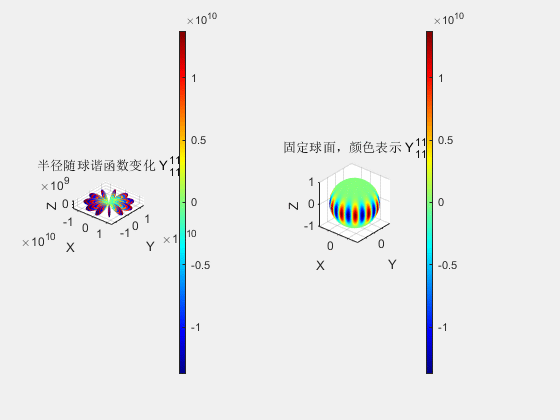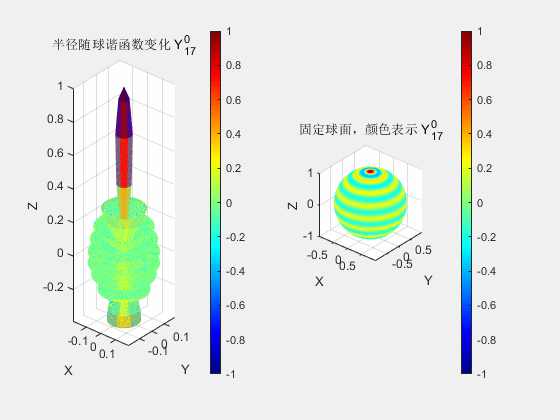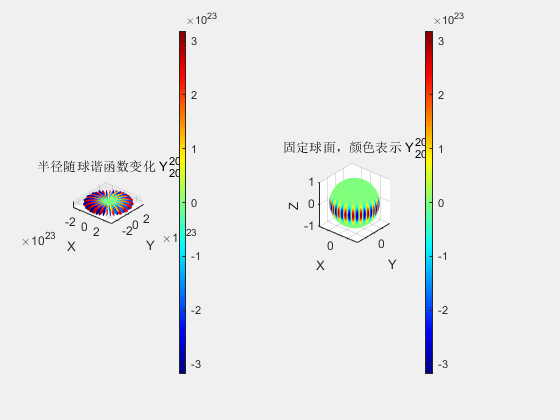
高斯椭球的颜色由球谐函数确定，高斯泼溅中以此实现不同视角下观察到不同颜色的效果。球谐函数是球坐标系下，定义在单位球面的一组具有正交完备性和旋转不变性的基函数。

之所以使用球坐标系函数，是为了将颜色与观测角度建立联系。而基函数是函数空间中的概念，基函数在其中的作用与向量空间中基向量的作用相同，即基函数可以通过线性组合张成函数空间中的任意函数(其实函数空间就是一种抽象的向量空间，同样满足向量空间中诸如对加法和数乘封闭等一系列性质)。球谐函数是球坐标系下的基函数，类似于笛卡尔坐标系下傅里叶级数中的\(\cos(nx)\)和\(\sin(nx)\)的概念，任何球面坐标系的函数都可以展开为无穷个球谐函数，换句话说，多个球谐函数的线性组合，可以近似表示任意的球坐标函数。

球谐函数本身，是球坐标系下的拉普拉斯方程在分离变量\(r\)后，角度部分通解的正交项。

\[\begin{aligned} 球坐标拉普拉斯方程:&\nabla^2 f = \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial f}{\partial r} \right) + \frac{1}{r^2 \sin\theta} \frac{\partial}{\partial \theta} \left( \sin\theta \frac{\partial f}{\partial \theta} \right) + \frac{1}{r^2 \sin^2\theta} \frac{\partial^2 f}{\partial \varphi^2}\\ 分离变量后角度部分的方程:& \frac{1}{\sin\theta} \frac{\partial}{\partial\theta} \left( \sin\theta \frac{\partial Y}{\partial\theta} \right) + \frac{1}{\sin^2\theta} \frac{\partial^2 Y}{\partial\varphi^2} + l(l + 1)Y = 0\quad (球函数方程)\\ \end{aligned}\]

球函数方程可以进一步分离变量，最终得到两个常微分方程，分别求解再回代可以得到球函数方程的解如下。其中关于方位角\(\theta\)的方程又称为连带勒让德方程，方程的解称为连带勒让德函数\(P_l^m (x)\)，全名为\(l\)次\(m\)阶连带勒让德函数(\(\text{degree} = l, \text{order} = m\))，在计算机中以递推的方式实现。

\[\begin{aligned} 球函数方程:&Y(\theta, \varphi) = \Theta(\theta) \Phi(\varphi) \\ 解得:&\Phi(\varphi) = \text{e}^{\text{i} m\varphi} ,\, m = 0, \pm 1, \cdots, \pm l &\quad(极角方程的解)\\ &\Theta(\theta) = P_l^m (\cos\theta) ,\, m = 0, \pm 1, \cdots, \pm l &\quad(方位角方程的解)\\ 其中&P_l^m(x) = (-1)^m (1 - x^2)^{\frac{m}{2}} \frac{\text{d}^m}{\text{d}x^m} \left(P_l(x)\right)&\quad(递推公式)\\ &P_l(x) = \frac{1}{2^l \cdot l!} \frac{\text{d}^l}{\text{d}x^l} \left[(x^2 - 1)^l\right]&\quad(通项公式)\\ 球函数方程的解为:&Y(\theta, \varphi) = \sum_{l=0}^{\infty} \sum_{m=-l}^{l} P_l^m (\cos\theta) \text{e}^{\text{i} m\varphi}, \, m = 0, \pm 1, \pm 2, \cdots \\ \end{aligned}\]

高斯泼溅中使用的是归一化的球谐函数的分量，归一化即在球函数方程解的基础上增加了归一化系数，分量是指在\(m>0\)时取\(\text{e}\)指数的实数部分，\(m<0\)时取\(\text{e}\)指数的虚数部分，最终得到高斯泼溅中球谐函数的表达式如下。

\[\begin{aligned} Y_l^m (\theta, \varphi) &= K_l^m Y_{lm} (\theta, \varphi)\\ &=\begin{cases} \sqrt{2} K_l^m \cos(m\varphi) P_l^m(\cos\theta) & m > 0 \\ \sqrt{2} K_l^m \sin(-m\varphi) P_l^{-m}(\cos\theta) & m < 0 \\ K_l^0 P_l^0(\cos\theta) & m = 0 \end{cases}\\ 其中K_l^m &= \sqrt{ \frac{2l + 1}{4\pi} \frac{(l - |m|)!}{(l + |m|)!} }\\ \end{aligned}\]

解释完了球谐函数本身，再聊聊正交完备性和旋转不变性。正交完备性包括正交归一性和完备性两个性质。函数空间的正交归一性定义为不同函数在定义域上的内积为 0，函数自身的内积为 1。完备性是指函数展开为基函数表示时，当次数趋于无穷时，级数和平均收敛于原函数，这保证了展开结果会趋近于被展开的函数。而旋转不变性是指，当原函数发生旋转时，只需对生成原函数的线性组合系数(也称为广义傅里叶系数)进行相应的变换，就可以保证变换后的系数能等价还原出新函数，而无需对新函数进行展开并计算广义傅里叶系数(生成系数的计算开销很大)。这具体表现为，当光源发生旋转时，只要同步计算出变换后的广义傅里叶系数，就能保证画面的光照效果不会抖动跳变。

对于给定的球谐函数次数，球谐函数和对应的球谐系数的数量是确定的，用于表示颜色的原函数可以按如下式子展开(以高斯泼溅中支持的最高次数三次为例)，其中球谐函数线性组合的系数就称为球谐系数。由原函数生成线性组合系数的过程称为投影，而用系数和基函数组合成原函数这个逆过程称为重建。

\[\begin{aligned} f &= \sum_{l} \sum_{m=-l}^{l} \mathbf{c}_{l}^{m} y_{l}^{m}(\theta, \phi) \\ &= \mathbf{c}_{0}^{0} y_{0}^{0}+ \\ &\quad \mathbf{c}_{1}^{-1} y_{1}^{-1}+\mathbf{c}_{1}^{0} y_{1}^{0}+\mathbf{c}_{1}^{1} y_{1}^{1}+ \\ &\quad \mathbf{c}_{2}^{-2} y_{2}^{-2}+\mathbf{c}_{2}^{-1} y_{2}^{-1}+\mathbf{c}_{2}^{0} y_{2}^{0}+\mathbf{c}_{2}^{1} y_{2}^{1}+\mathbf{c}_{2}^{2} y_{2}^{2}+ \\ &\quad \mathbf{c}_{3}^{-3} y_{3}^{-3}+\mathbf{c}_{3}^{-2} y_{3}^{-2}+\mathbf{c}_{3}^{-1} y_{3}^{-1}+\mathbf{c}_{3}^{0} y_{3}^{0}+\mathbf{c}_{3}^{1} y_{3}^{1}+\mathbf{c}_{3}^{2} y_{3}^{2}+\mathbf{c}_{3}^{3} y_{3}^{3} \end{aligned}\]

与函数的傅里叶级数类似，球谐函数的次数\(l\)越高，实现的颜色表达就越细致。在三阶的情况下，按 RGB 三通道计算，完整的球谐系数存储为一个\(3\times 16\)的矩阵。

高斯椭球渲染

高斯椭球是三维场景结构的表示，需要一定的步骤将其转化到二维图像平面。从具体操作上来说，其实是将高斯椭球的所有参数转化到二维平面，再离散到像素上。位置和协方差使用不同的处理管线，颜色和不透明度不涉及维度的概念，因此也不需要所谓的转化，颜色只需按给定的观察方位和高斯的球谐系数分别计算颜色的 rgb 分量即可，不透明度在这一步无需处理。(注：不透明度用于后续合成图像时的 \(\alpha\)-blending，为了叙述方便，将这部分内容划分到后面的“并行渲染管线”章节介绍，故不在这里涉及不透明度的处理。)

位置处理管线

对于位置参数，采用世界坐标系–>相机坐标系–>归一化设备坐标系–>像素坐标系的流程。

由于高斯椭球中的位置表示在 world frame(世界坐标系)下，而图像是针对于某个具体的相机视角的，因此需要先将位置的表示方式从 world frame 转化到 camera frame 下，这一步转换称为观测变换，简称 W2C(world to camera)。

转换是坐标系之间的变换，实质是平移和旋转的合成，而为了将两个操作合为一个矩阵，将空间位置用齐次向量\([x, y, z, 1]^\top\)表示。根据从 COLMAP 中得到的表示平移的向量\(\text{tvec} = [t_x, t_y, t_z]^\top\)，和表示旋转的四元数\(\text{qvec} = \{q_0, q_1, q_2, q_3\}\)得到的旋转矩阵\(\mathbf{R}=\begin{bmatrix} r_{xx} & r_{xy} & r_{xz} \\ r_{yx} & r_{yy} & r_{yz} \\ r_{zx} & r_{zy} & r_{zz} \end{bmatrix}\)(四元数转旋转矩阵的过程有固定的计算步骤，此处省略；另外，高斯泼溅中所有的四元数转旋转矩阵的计算均使用右手系下的公式)，可以按如下方式构造 W2C 的变换矩阵\(\text{view matrix}\)(完整的 W2C 矩阵推导过程可见参考资料，此处只给出由 tvec 和 qvec 构造矩阵的过程)。不难发现，W2C 变换矩阵其实就是相机的外参矩阵

\[\text{view matrix} = \begin{bmatrix} r_{xx} & r_{xy} & r_{xz} & t_x \\ r_{yx} & r_{yy} & r_{yz} & t_y \\ r_{zx} & r_{zy} & r_{zz} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\\\]

不妨假设位置在世界坐标系下表示为\([x_w, y_w, z_w, 1]^\top\)，在相机坐标系下表示为\([x_c, y_c, z_c, 1]^\top\)，则通过以下坐标变换可以得到相机坐标系下的位置表示

\[\begin{bmatrix} x_c\\ y_c\\ z_c\\ 1 \end{bmatrix} = \begin{bmatrix} r_{xx} & r_{xy} & r_{xz} & t_x \\ r_{yx} & r_{yy} & r_{yz} & t_y \\ r_{zx} & r_{zy} & r_{zz} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\\ \begin{bmatrix} x_w\\ y_w\\ z_w\\ 1 \end{bmatrix}\]

值得注意的是，从 COLMAP 中得到的 qvec 和 tvec 是 W2C 的，即 qvec 表示世界系的基底在相机系中的姿态(且已经做了归一化)，tvec 表示世界系的原点在相机系中的位置。以坐标变换来理解，设世界系为旧基，世界系下坐标为\(\mathbf{x}=(x_1, x_2, \cdots, x_n)^\top\)；相机系为新基，相机系下坐标为\(\mathbf{y}=(y_1, y_2, \cdots, y_n)^\top\)；过渡矩阵\(\mathbf{P}\)为用世界系表示相机系的变换矩阵，那么 qvec 对应的旋转矩阵和 tvec 对应的平移向量构成的变换矩阵是用相机系表示世界系的变换矩阵，即\(\mathbf{P}^{-1}\)。根据坐标变换公式\(\mathbf{y} = \mathbf{P}^{-1} \mathbf{x}\)，因此\(\mathbf{P}^{-1}\)记为 W2C 矩阵，即世界坐标系转换到相机坐标系的变换矩阵；而如果想获得相机在世界坐标系下的位置，则应该从过渡矩阵\(\mathbf{P}\)取。另外，由于 CUDA 中矩阵的内存布局为列主序；而 torch 和 numpy 中矩阵的布局均为行主序，因此需要传入 CUDA 部分参与运算的 view matrix 和 projection matrix 在代码中均进行了转置。

转化到相机坐标系之后，还需要投影到二维平面，这一步骤称为投影变换，具体来说是透视投影变换。投影变换的具体操作，是用内参构造投影矩阵(注意不是使用内参矩阵)，再用这个矩阵将坐标从相机坐标系变换到 NDC(Normalized Device Coordinate，归一化坐标系；另外，此处的投影变换指的是计算机图形学范畴的概念，是将相机坐标系转化到 NDC 的步骤；后文关于协方差处理中的投影变换，则是指计算机视觉中的概念，即将相机坐标系转化到图像平面上的步骤)。所谓的 NDC，在不同的图形学 API 中定义不同，OpenGL 和 glm 中定义为\([-1, 1]^3\)的右手系立方体空间，DirectX 中定义为\([-1, 1]^2, z \in [0, 1]\)的左手系长方体空间，不同的 NDC 定义，推导出的投影矩阵是有差别的。高斯泼溅中使用 DirectX 的定义，将 znear 平面映射到 z=0 平面，zfar 平面映射到 z=1 平面。

在这样的规定下，结合由视锥范围计算出的\(t、b、l、r\)，记近平面和远平面的 z 值分别为 n 和 f，推导出投影矩阵\(\text{projection matrix}\)如下(推导过程可见参考资料，此处省略；另外，投影矩阵的推导方式有两种，一种是按照 GAMES 101 中的方式先将视锥非线性压缩为长方体再正交投影到 NDC，另一种是直接推导投影矩阵；两种方式的推导结果在[0,2]和[1, 2]两个元素上相差一个负号，相当于将变换之后的图像旋转 180°，对高斯椭球的参数学习没有影响；此处列出的为前一种推导方式的结果)

\[\text{projection matrix} = \begin{bmatrix} \displaystyle \frac{2n}{\,r-l\,} & 0 & \displaystyle -\frac{r+l}{\,r-l\,} & 0 \\[8pt] 0 & \displaystyle \frac{2n}{\,t-b\,} & \displaystyle -\frac{t+b}{\,t-b\,} & 0 \\[8pt] 0 & 0 & \displaystyle \frac{f}{\,n-f\,} & \displaystyle -\frac{nf}{\,n-f\,} \\[8pt] 0 & 0 & 1 & 0 \end{bmatrix}\]

(注：内参矩阵是计算机视觉的概念，直接将三维空间转化到像素平面，用于只关心真实的像素投影的情况；而计算机图形学中一般会先转化到 NDC 坐标系，主要是为了兼容不同的屏幕分辨率，降低渲染管线的耦合度。后续图形硬件对空间进行裁剪做可见性测试以及硬件栅格化都可以针对这个统一的空间进行，最后再单独映射到屏幕分辨率，避免了与分辨率产生耦合。高斯泼溅中使用了这套渲染管线，因此使用投影矩阵而不是内参矩阵。)

不妨假设位置在相机坐标系下表示为\([x_w, y_w, z_w, 1]^\top\)，在 NDC 坐标系下表示为\([x_n, y_n, z_n, w_n]^\top\)，则通过以下坐标变换可以得到相机坐标系下的位置表示

\[\begin{bmatrix} x_n\\ y_n\\ z_n\\ w_n \end{bmatrix} = \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{f}{n-f} & -\frac{nf}{n-f} \\ 0 & 0 & 1 & 0 \end{bmatrix}\\ \begin{bmatrix} x_c\\ y_c\\ z_c\\ 1 \end{bmatrix}\]

对于齐次坐标，所有分量同时除以同一个数得到的结果与原坐标等价；为了保证 w 分量保持为 1，对结果同时除以\(w_n\)，即\([x_n, y_n, z_n, w_n]^\top = [\frac{x_n}{w_n}, \frac{y_n}{w_n}, \frac{z_n}{w_n}, 1]^\top\)，这一步称为透视除法。

由于后续只关心屏幕空间二维投影，故只取结果的 x 和 y 分量，相当于转化到图像坐标系。此时已经将三维椭球转化到了\([-1, 1]^2\)的平面范围内，而图像尺寸是\([w, h]\)，因此还需要拉伸回这个尺寸；此外，图像坐标系的原点在图像正中心，目标的像素坐标系在图像的左上角，因此相差一个平移。这两步合起来将\([-1, 1]^2\)的平面坐标系转化到像素坐标系，称为视口变换。不妨假设位置在\([-1, 1]^2\)平面范围内表示为\((x_n, y_n)\)，在像素坐标系下表示为\((x_p, y_p)\)，则视口变化可以表示为

\[\begin{aligned} x_p = \frac{w}{2}\cdot x_n + \frac{w}{2}\\ y_p = \frac{h}{2}\cdot y_n + \frac{h}{2}\\ \end{aligned}\]

但考虑到下一步的像素离散操作，需要从不考虑面积的点转化到有面积的像素上，所以这一步在代码实现中其实将 NDC 中的点映射到了像素中心而不是边缘，避免了边界处偏移半像素的问题。对于索引为\((i, j)\)的像素，像素中心为\((i+0.5, j+0.5)\)，因此在上述转化的基础上只需偏移 0.5 个单位即可。另外需要注意的是，像素索引范围等于像素坐标或者说像素数量 - 1。以一维的四个像素为例说明这一点，浅蓝色代表像素索引，浅绿色代表像素坐标，同时也是像素范围。

高斯泼溅的代码中使用向左偏移 0.5 个单位的写法，将\((-1, 1)\)映射到\((-0.5, \text{width}-0.5)\)，而不是\((0.5, \text{width}+0.5)\)。映射到\((-0.5, \text{width}-0.5)\)之后再转为 int 截去小数部分(截取小数部分的操作对正数相当于向下取整，对负数则是向上取整)，这样正好使得索引控制在\([0, \text{width}-1] \times [0, \text{height}-1]\)。反之如果映射到\((0.5, \text{width}+0.5)\)，就需要编写额外的逻辑来去掉多出来的像素。

协方差处理管线

对于形状参数，采用世界坐标系–>相机坐标系–>图像平面坐标系的流程，具体来说是将协方差矩阵进行层层传递的过程。

首先根据旋转四元数转化得到的旋转矩阵\(\mathbf{R}\)和三个主轴的缩放\(\sigma_i\)构造世界坐标系下的三维协方差矩阵\(\mathbf{V}_k'' = \mathbf{R}~ \cdot\text{diag}(\sigma_1^2 \, \sigma_2^2 \, \sigma_3^2)\cdot ~\mathbf{R}^\top\)

世界坐标系到相机坐标系的转化为观测变换，本质上是平移+旋转构成仿射变换。高斯协方差矩阵在仿射变换下的规律如下(推导过程见 EWA Volume Splatting，此处直接给出结论)，将位置\(\mathbf{t}_k\)处、形状为协方差矩阵\(\mathbf{V}_k''\)的高斯 kernel 记为

\[r_k''(t) = G_{\mathbf{V}_k''}(\mathbf{t}-\mathbf{t}_k) = \frac{1}{2|\mathbf{V}_k''|^{-\frac{1}{2}}}\text{exp}\left( \left(\mathbf{t}-\mathbf{t}_k\right)^\top \mathbf{V}_k''^{-1} \left(\mathbf{t}-\mathbf{t}_k\right) \right)\]

设仿射变换为\(\mathbf{u} = \varphi(\mathbf{t}) = \mathbf{W}\mathbf{t} + \mathbf{d}\)，变换前后的高斯 kernel 满足如下等式，可见变换之后协方差矩阵传递为\(\mathbf{W}\mathbf{V}_k'\mathbf{W}^\top\)

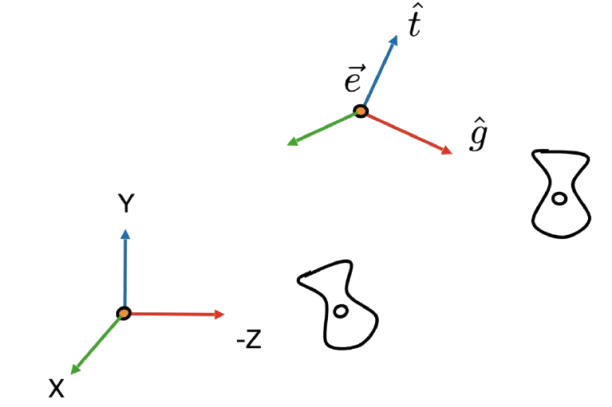
\[G_{\mathbf{V}_k''}(\varphi^{-1}(\mathbf{u})-\mathbf{t}_k) = \frac{1}{|\mathbf{W}^{-1}|}G_{\mathbf{V}_k'}(\mathbf{u}-\mathbf{u}_k) = r_k'(u), 其中\mathbf{V}_k' = \mathbf{W}\mathbf{V}_k''\mathbf{W}^\top\\\]

为了处理非线性的投影变换，高斯泼溅中采用了 EWA Volume 中的方法，先将相机空间变换到投影平面为图像平面的光线空间，再用局部仿射变换来近似投影变换。为了理解推导过程，需要先介绍这个所谓的光线空间。光线空间是用于参数化所有可能光线的非线性空间，以下的介绍针对 EWA Volume Splatting 中的光线空间，与计算机图形学或计算机视觉中一般意义上的光线空间有区别。给定投影中心和投影平面，从投影中心发出光线穿过投影平面，令光线空间中，点的坐标为\(\mathbf{x} = [x_0, x_1, x_2]^\top\)。这三个坐标分量的含义如下：穿过投影中心和投影平面上坐标为\((x_0, x_1)\)的点的光线称为观测光线；\(x_2\)表示从投影中心出发，沿观测光线方向、移动\(x_2\)的欧式距离到达该点。光线空间可以看作视锥的参数化描述；光线由像素位置决定，点的位置由光线方向和距离决定。

EWA Volume Splatting 指出，通过将相机空间变换到这样的光线空间，可以将非线性的投影变换在局部近似为仿射变换这样的线性变换(这里的线性变换是指变换将直线映射为直线，不是线性代数意义上的线性变换)。在相机空间下，直接进行透视投影需要除以深度，引入了非线性，雅可比矩阵对深度变化敏感，不适合用局部线性近似的方式来处理；转化到光线空间后，由于深度信息在光线空间的方向向量表示下被归一化掉了，深度在光线空间表现为线性缩放，可以采用局部线性近似处理。之所以是局部近似，是因为近似的实质是泰勒一阶展开，只对光线穿过的点是精确的，而对于整个投影的对象，并不能在全局采用这种近似方法。这种局部一阶近似提供了一种高效执行透视投影的方式，可实现与 OpenGL 中投影变换相同的功能。

高斯泼溅中将投影平面设为图像平面，该平面到投影中心的距离为焦距\(f\)，由于要将空间坐标映射到图像平面，故需要用水平像素尺寸下的表示\(f_x\)和竖直像素尺寸下的表示\(f_y\)。设空间点的在相机空间下的坐标表示为\(\mathbf{u} = [u_0, u_1, u_2]^\top\)，在光线空间下的坐标表示为\(\mathbf{x} = [x_0, x_1, x_2]^\top\)，两者映射关系记为\(\mathbf{x} = m(\mathbf{u})\)，令\(l = \vert\vert(u_0, u_1, u_2)^\top\vert\vert\)

\[\begin{aligned} \begin{bmatrix} x_0\\ x_1\\ x_2 \end{bmatrix} = m(\mathbf{u}) = \begin{bmatrix} f_x \frac{u_0}{u_2}\\ f_y \frac{u_1}{u_2}\\ l \end{bmatrix} \end{aligned}\]

通过这样的映射，即可将相机空间投影到图像平面，代替了直接进行透视投影的操作；而这一步映射本身也是非线性的，用局部仿射变换来近似表示。局部仿射变换定义为\(m(\mathbf{u})\)在\(\mathbf{u}_k\)处的一阶泰勒展开，根据雅可比矩阵的定义，计算向量对向量的导数可以求出雅可比矩阵

\[\begin{aligned} \mathbf{x} = m_{\mathbf{u}_k}(\mathbf{u}) &= \mathbf{x}_k + \mathbf{J}_{\mathbf{u}_k}(\mathbf{u} - \mathbf{u}_k), 其中 \mathbf{J}_{\mathbf{u}_k} = \left. \frac{\partial m(\mathbf{u})}{\partial \mathbf{u}} \right|_{\mathbf{u} = \mathbf{u}_k}, \mathbf{x}_k = m(\mathbf{u}_k)\\ \mathbf{J}_{\mathbf{u}_k} &= \begin{bmatrix} \displaystyle \frac{\partial m_1(\mathbf{u})}{\partial u_1} & \displaystyle \frac{\partial m_1(\mathbf{u})}{\partial u_2} & \displaystyle \frac{\partial m_1(\mathbf{u})}{\partial u_3} \\[8pt] \displaystyle \frac{\partial m_2(\mathbf{u})}{\partial u_1} & \displaystyle \frac{\partial m_2(\mathbf{u})}{\partial u_2} & \displaystyle \frac{\partial m_2(\mathbf{u})}{\partial u_3} \\[8pt] \displaystyle \frac{\partial m_3(\mathbf{u})}{\partial u_1} & \displaystyle \frac{\partial m_3(\mathbf{u})}{\partial u_2} & \displaystyle \frac{\partial m_3(\mathbf{u})}{\partial u_3} \end{bmatrix} = \begin{bmatrix} \displaystyle \frac{f_x}{u_2} & \displaystyle 0 & \displaystyle -\frac{f_x u_0}{u_2^2} \\[8pt] \displaystyle 0 & \displaystyle \frac{f_y}{u_2} & \displaystyle -\frac{f_y u_1}{u_2^2} \\[8pt] \displaystyle \frac{u_0}{l} & \displaystyle \frac{u_1}{l} & \displaystyle \frac{u_2}{l} \\[8pt] \end{bmatrix} \end{aligned}\]

根据前面的高斯协方差矩阵在仿射变换下的规律，应用局部仿射变换前后的高斯 kernel 满足如下等式，变换之后协方差矩阵传递为\(\mathbf{J}\mathbf{W}\mathbf{V}_k''\mathbf{W}^\top\mathbf{J}^\top\)

\[G_{\mathbf{V}_k'}(m^{-1}(\mathbf{x})-\mathbf{u}_k) = \frac{1}{|\mathbf{J}^{-1}|}G_{\mathbf{V}_k}(\mathbf{x}-\mathbf{x}_k) = r_k(x), 其中\mathbf{V}_k = \mathbf{J}\mathbf{V}_k'\mathbf{J}^\top = \mathbf{J}\mathbf{W}\mathbf{V}_k''\mathbf{W}^\top\mathbf{J}^\top\\\]

由于后续处理只关心二维高斯椭圆的协方差矩阵，因此代码实现时会将雅可比矩阵的第三行置零，最终结果矩阵左上角\(2\times 2\)的分块矩阵作为二维协方差，记为\(\mathbf{\Sigma}\)，至此便得到了高斯椭球渲染到图像平面的 footprint。后续计算中会使用\(\mathbf{\Sigma}^{-1}\)，因此在代码中 preprocess 部分会进行求逆，并将结果记为为\(\text{conic}\)。

光栅化并行渲染管线

光栅化是计算机图形学中，将连续的三维几何场景转换为离散的屏幕像素的图形处理管线；高斯泼溅中为了加速光栅化的渲染过程，基于 torch 的 CUDA 接口提供了 GPU 并行的编程实现。

GPU 并行编程基础

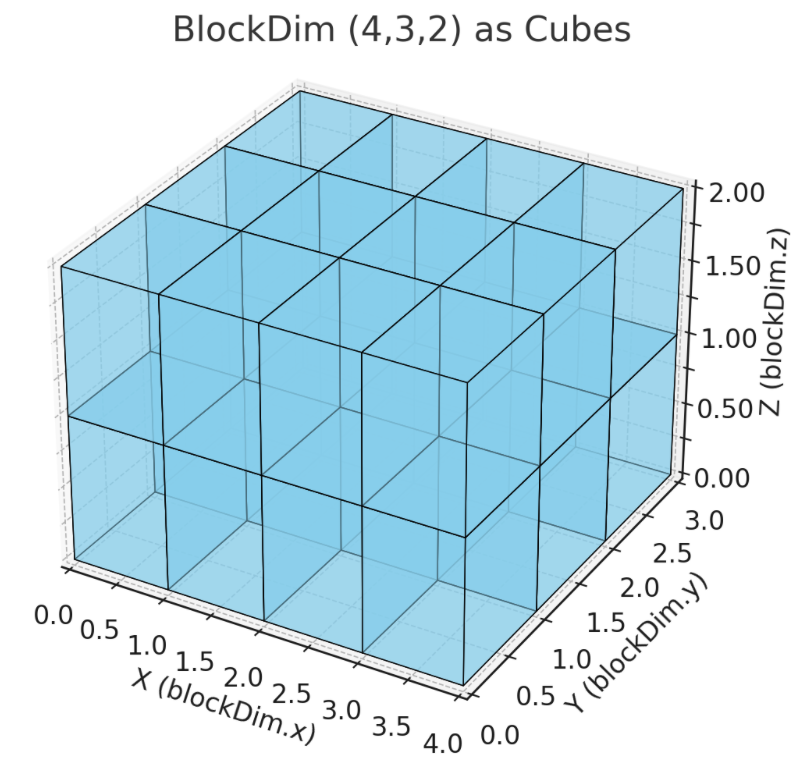
为了理清这部分的逻辑，有必要先介绍最基本的 GPU 并行编程概念。GPU 上并行执行的指令称为核函数；CUDA 在逻辑访问上的层级结构分为 grid、block 和 thread 三级。grid 下分为多个 block，一个 block 中包含多个 thread，一个 block 内可以使用共享内存(共享内存是 GPU 中比全局内存访问速度快得多的一种存储结构，但大小十分有限)。block size 表示一个 block 内含有的 thread 数，block dim 表示 block 内线 thread 的组织结构。组织结构可以这样理解，把一个 thread 想象成一个边长为 1 的小立方体，block dim = (4, 3, 2)表示立方体排列成长宽高分别为 4、3、2 的长方体，如下图所示。组织结构支持一维到三维，未指定的维度默认设置为 1。类似地，gird size 表示一个 grid 内含有的 block 数，grid dim 表示 grid 内 block 的组织结构。核函数以整个 gird 为范围、以 thread 为单位执行，即每个线程都会运行一次核函数，多个线程同时运行核函数即可实现并行数据处理。

并行渲染策略

高斯泼溅中将图像按分辨率向上取整划分为多个 tile，每个 tile 包含 16*16=256 个像素。整个并行逻辑分为 preprocess 和 render 两部分，preprocess 部分每个 thread 负责一个高斯椭球，block size 设置为(256, 1, 1)，grid size 根据高斯椭球总数进行设置；render 部分每个 thread 负责一个像素，且每个 block 负责一个 tile，block size 设为(16, 16, 1)，与 tile 中的像素对应，grid size 根据划分出的 tile 数进行设置。

例如，图像分辨率为 1920*1080，高斯总数为 30000，\(\left\lceil x \right\rceil\)为向上取整的符号，上述过程计算如下：

\[\begin{aligned} &\text{preprocess}部分的\text{block size}为: (256, 1, 1)\\ &\text{preprocess}部分的\text{grid size}为: \left\lceil\frac{30000}{256}\right\rceil = 118 \Rightarrow (118, 1, 1)\\ &\text{render}部分的\text{block size}为: (16, 16, 1)\\ &划分的\text{tile}数: \left\lceil \frac{1920}{16} \right\rceil \times \left\lceil \frac{1080}{16} \right\rceil = 120 \times 68 = 8160\\ &\text{render}部分的\text{grid size}为: (120, 68, 1)\\ \end{aligned}\]

在 preprocess 部分，以某一个 thread 为例，按照前面介绍的高斯椭球转化过程，计算得到像素坐标系下的高斯椭圆，即 xy 位置和距离相机的深度、2D 协方差矩阵、颜色和不透明度。接下来需要得到这个高斯椭圆所涉及的 tile 索引范围和数量，为此对二维协方差进行特征值分解，取最大特征值的三倍(即高斯函数中的\(3\sigma\))这个范围的 AABB(Axis Aligned Bounding Box，轴对齐包围盒，是边与坐标轴平行的外切矩形，可由一组点中的最小坐标和最大坐标确定)作为该高斯椭圆的影响区域，记录该区域涉及的 tile 索引范围且可以据此得出高斯椭圆影响的 tile 数量。

将所有高斯椭圆涉及的 tile 数求和，就是实际要处理的渲染任务总数。在高斯泼溅中，这些椭圆按照到相机的距离从近到远的顺序渲染到图像上，完成全部高斯椭球的处理后的结构类似于下图。高斯椭圆和 tile 之间是多对多的关系，即一个高斯椭圆可能影响多个 tile，一个 tile 也可能受多个高斯椭圆影响。

为了处理这种多对多的关系并实现这种按深度顺序进行渲染的逻辑，构造 \(tile id \vert depth <----> gaussian id\) 的键值对，将 tile 索引置于键的高位，深度置于键的低位，高斯椭圆的索引作为值构成一条 entry。这样的 entry 假定一个高斯椭圆影响一个 tile，根据高斯椭圆影响 tile 的数量对其进行复制，如某个高斯椭圆影响 5 个 tile，则将其复制 5 份并分别构造 entry(注：这里的复制只是一种理解方式，指的是重复使用这个高斯索引来与它影响的不同 tile 分别构成 entry，而不是在内存上将高斯参数进行复制)。对这个 entry 表进行键值对的排序，就可以将高斯索引按 tile 索引排列好，同一个 tile 内按深度排列好，举例如下图。

(注：高斯泼溅在构建这样的 entry 时其实还会根据高斯椭圆对 tile 的贡献值进行排序，小于一定阈值则认为影响可以忽略，并不会构造这个 entry。具体来说是，对某一个椭圆影响的某一个 tile，按照椭圆梯度的方法计算这个 tile 内高斯函数的最大值，大于阈值才认为这个椭圆对这个 tile 有贡献，才会构建这个 entry。)

排序完成之后，就获得了每个 tile 上需要处理的高斯椭圆的索引，接下来进入每个 thread 负责一个像素、每个 block 负责一个 tile 的 render 部分。在一个 tile 内，为了利用 GPU 的共享内存机制，对所有的高斯椭圆进行分轮次处理，每一轮处理前都先将数据读入共享内存，高斯泼溅中将每一轮处理的高斯数量设为 256。在一个轮次内，遍历这 256 个高斯椭圆，计算它们对这个 tile 内所有像素的影响。对某一个高斯椭圆来说，一个线程处理一个像素，整个 block 内的 thread 并行即可处理完某一个高斯椭圆对整个 tile 的影响。由此经过轮次的循环和高斯椭圆的循环，即可处理完整个 tile 上所有高斯椭圆对这个 tile 中所有像素的影响。

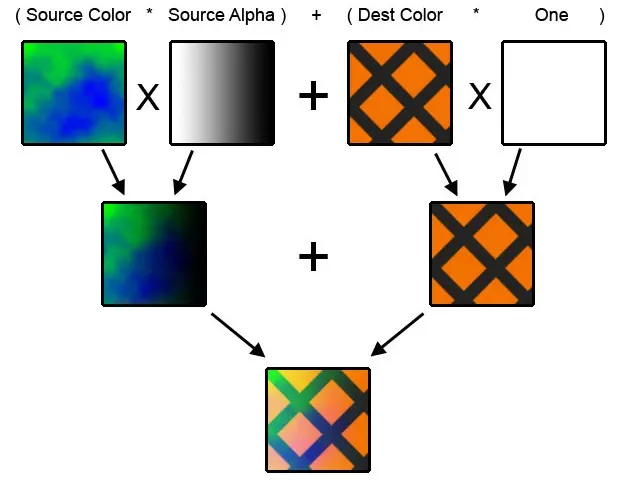
\(\alpha\)-blending 图像合成

一个轮次中的 256 个高斯椭圆对这个 tile 中某一个像素的颜色累积过程称为\(\alpha-\text{blending}\)。每个椭圆参与合成的实际\(\alpha\)，由像素中心和高斯函数中心之间的马氏距离进行椭圆平均加权。

椭圆加权平均(EWA)是一种高质量的采样和抗锯齿算法，适合处理椭圆形状分布的元素，核心思想是基于二维协方差的马氏距离。马氏距离是一种距离指标，可以应对高维线性分布的数据中各维度间非独立同分布的问题，修正了欧式距离中各维度尺度不一致且相关的问题，本质上是对 PCA 中的主成分进行标准化，将变量按主成分旋转(主成分就是特征向量的方向)，使各维度之间相互独立，然后再标准化(缩放特征值)使它们同分布。马氏距离其实就是标准化之后的欧式距离。

\[\begin{aligned} D_M(\mathbf{x}) &= \sqrt{(\mathbf{x} - \mathbf{\mu})^\top\Sigma^{-1}(\mathbf{x} - \mathbf{\mu})}\\ D_M(\mathbf{x}, \mathbf{y}) &= \sqrt{(\mathbf{x} - \mathbf{y})^\top\Sigma^{-1}(\mathbf{x} - \mathbf{y})}\\ 二维高斯函数: G(\mathbf{x}) &= \frac{1}{2\pi \sqrt{|\mathbf{\Sigma}|}} \exp\left( -\frac{1}{2} (\mathbf{x} - \mathbf{\mu})^\top \mathbf{\Sigma}^{-1} (\mathbf{x} - \mathbf{\mu}) \right),\\ \text{其中 } \mathbf{x} &= \begin{bmatrix} x_1 \\ x_2 \end{bmatrix},\quad \mathbf{\mu} = \begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix},\quad \mathbf{\Sigma} = \begin{bmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{bmatrix}\\ \end{aligned}\]

设高斯椭圆中心坐标为\((\text{center}_x, \text{center}_y)\)，像素中心坐标为\((\text{pixel}_x, \text{pixel}_y)\)，EWA 中权重的计算公式如下，其中\(\mathbf{\Sigma}\)为高斯椭圆的协方差矩阵。

\[\begin{aligned} \begin{bmatrix} d_x\\ d_y\\ \end{bmatrix} &= \begin{bmatrix} \text{center}_x\\ \text{center}_y\\ \end{bmatrix} - \begin{bmatrix} \text{pixel}_x\\ \text{pixel}_y\\ \end{bmatrix} \\ \text{power} &= -\frac{1}{2}(D_M(\text{center}, \text{pixel}))^2 = -\frac{1}{2}\left( \begin{bmatrix} d_x & d_y \end{bmatrix} \mathbf{\Sigma}^{-1} \begin{bmatrix} d_x\\ d_y\\ \end{bmatrix} \right)\\ \end{aligned}\]

像素颜色累积公式如下，其中\(C\)为像素颜色，\(c\)为高斯椭圆颜色；\(\alpha\)为高斯椭圆对像素的透明度贡献，即参与合成的实际\(\alpha\)；\(T\)为像素在接受当前高斯椭圆渲染之前的透射率，即像素的剩余透明度。事实上，颜色值的更新，就是在当前处理的高斯椭圆颜色值，和截止当前的颜色累积值之间进行插值的过程。

\[\begin{aligned} 颜色更新:\quad &C_\text{final}= c_i\cdot\alpha_i+c_\text{accum}\cdot(1 - \alpha_i) \quad &即C=\sum_{i = 1}^{N} T_i\alpha_i c_i\\ 剩余透明度更新:\quad &T_\text{final}=T_\text{accum}\cdot(1 - \alpha_i) \quad &即T_i= \prod_{j = 1}^{i - 1} (1 - \alpha_j)\\ \end{aligned}\]

颜色积累的迭代更新实现见如下伪代码，值得注意的是：第一，透明度贡献\(\alpha\)大于阈值的高斯椭圆才会参与对当前像素的渲染，这就是所谓的像素离散，将连续的高斯椭圆离散渲染到屏幕像素上。第二，剩余透明度\(T\)小于阈值时，表示对于当前像素而言，前面的高斯椭圆已经将光吸收完了，后面的高斯椭圆对该像素的颜色不再有贡献。