3DGS原理
3DGS前置知识
概述
3DGS 是基于 Splatting 和机器学习的三维重建方法，从 SfM 生成的点云出发，将点膨胀成三维高斯椭球，再通过光栅化投影到二维平面，与真值图像 GT 作 loss，计算梯度反向传播以调整优化高斯椭球的参数，最终得到完整的场景描述。损失函数如下 \(L = (1-\lambda)L_1 + \lambda L_{D-SSIM}，原版\text{3DGS}中取\lambda=0.2\)
3DGS 中的 Splatting 和 NeRF 中的 Ray-Casting 都是渲染的方法。前者是从粒子出发，计算每个粒子对像素的影响；后者是从像素出发，找到影响这个像素的发光粒子。
初始化
多视角图像经过SfM生成三维点云、每个点的颜色和相机内外参矩阵；然后通过KNN算法计算与之最近的三个点的平均距离（局部密度估计），并以此为半径初始化标准球形高斯（位置为点的位置、协方差矩阵为单位矩阵、颜色为点的颜色、不透明度统一设为较小值）；接着对于每个点的三个邻居计算局部点集协方差矩阵并作SVD分解得到主轴方向和轴长，并以此将初始高斯球调整为高斯椭球。KNN由simple-knn这一CUDA模块实现。
三维高斯表示
对于 SfM 获得的点云，使用三维的高斯函数进行膨胀，每个高斯椭球包含的参数有：中心位置、协方差矩阵、球谐系数、不透明度。之所以选择高斯椭球而不是立方体或球等其它函数来表示三维场景是因为高斯函数具有良好的数学性质，一是高斯函数对仿射变换封闭（渲染中需要用到仿射变换），二是三维高斯沿某一个轴积分成二维后仍为高斯函数（渲染实质上就是投影到二维平面）。
高斯函数的表达式如下（高维高斯均假设各向异性，即不同方向梯度不同）
\[\begin{aligned} G(x) &= \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(x - \mu)^2}{2\sigma^2} \right)\\ G(\boldsymbol{x}) &= \frac{1}{2\pi \sqrt{|\boldsymbol{\Sigma}|}} \exp\left( -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) \right),\\ &\text{其中 } \boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix},\quad \boldsymbol{\mu} = \begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix},\quad \boldsymbol{\Sigma} = \begin{bmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{bmatrix}\\ G(\boldsymbol{x}) &= \frac{1}{(2\pi)^{3/2} \sqrt{|\boldsymbol{\Sigma}|}} \exp\left( -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) \right),\\ &\text{其中 } \boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix},\quad \boldsymbol{\mu} = \begin{bmatrix} \mu_1 \\ \mu_2 \\ \mu_3 \end{bmatrix},\quad \boldsymbol{\Sigma} = \begin{bmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{bmatrix}\\ \boldsymbol{\mu}为均值&，决定分布的形状\\ \boldsymbol{\Sigma}为协方&差矩阵，为半正定的对称矩阵，对角线元素为方差，其余元素为协方差，决定分布的形状 \end{aligned}\]下面解释为什么三维高斯函数是椭球，首先以二维出发：令二维高斯函数为某一常数，提取各高次项系数并整理之后可以得到一个标准的椭圆方程；几何意义上理解更直观：想象一个平面与钟形曲面相交，截出的曲线就是椭圆。
三维高斯同理，令其为常数并提取各高次项系数，整理之后就是一个标准的椭球面方程。在几何意义上为了可视化出来，可以想象用颜色来代表函数值，这样，三维高斯函数就是一个实心椭球，从内到外就是颜色渐变的椭球壳。
任意高斯分布可由标准高斯分布通过仿射变换得到，对高斯进行仿射变换满足如下规律
\[\begin{aligned} \boldsymbol{x} &\sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})\\ \boldsymbol{y} &= \boldsymbol{A} \boldsymbol{x} + \boldsymbol{b}\\ \boldsymbol{y} &\sim \mathcal{N}(\boldsymbol{A} \boldsymbol{\mu} + \boldsymbol{b},\ \boldsymbol{A} \boldsymbol{\Sigma} \boldsymbol{A}^\top)\\ \end{aligned}\]对于标准正态分布，\(\boldsymbol{\Sigma}=\mathbf{I}\)，\(\boldsymbol{\Sigma’} = \boldsymbol{A}\mathbf{I}\boldsymbol{A}^\top = \boldsymbol{R}\boldsymbol{S}\boldsymbol{S}^\top\boldsymbol{R}^\top\)，由于仿射变换本身可以表达为旋转、缩放和平移（\(\boldsymbol{A} \boldsymbol{x} + \boldsymbol{b} = \boldsymbol{R}\boldsymbol{S} \boldsymbol{x} + \boldsymbol{b}\)）。综上所述，可以用旋转矩阵和缩放矩阵表达协方差矩阵。而之所以要这样分解，是为了在优化的过程中自然地满足协方差矩阵为半正定的对称矩阵这一约束（旋转矩阵为正交矩阵，满足转置等于逆的性质；而缩放矩阵为对角矩阵，实际合成为\(\boldsymbol{R}~ \text{diag}(\sigma_1^2\ \sigma_2^2\ \sigma_3^2) ~\boldsymbol{R}^\top\)）。已知协方差矩阵，也可以通过特征值分解（EVD）的方式求得相应的旋转矩阵和缩放矩阵。
为了将颜色与观测角度建立联系，引入球坐标系，因为球在不同方向上反射的光是不同的。球谐函数是球坐标系下定义在单位球面上的正交基函数，类似于笛卡尔坐标系下傅里叶级数中的\(\cos(nx)\)和\(\sin(nx)\)的概念，任何球面坐标系的函数都可以用多个球谐函数来近似，3DGS 中用球谐函数来描述环境中光的存在，实现对亮度的重建。
球谐函数展开如下，可实现不同角度观察得到不同颜色的效果。其中\(l\)为阶数，阶数越高颜色表达越细致，原版 3DGS 中取\(l=3\)。\(c_{l}^{m}\)为球谐系数，为三维向量，存储了 RGB 三通道颜色分量。在三阶的情况下，完整的球谐系数存储为一个\(3\times 16\)的矩阵
\[\begin{aligned} f &= \sum_{l} \sum_{m=-l}^{l} \boldsymbol{c}_{l}^{m} y_{l}^{m}(\theta, \phi) \\ &= \boldsymbol{c}_{0}^{0} y_{0}^{0}+ \\ &\quad \boldsymbol{c}_{1}^{-1} y_{1}^{-1}+\boldsymbol{c}_{1}^{0} y_{1}^{0}+\boldsymbol{c}_{1}^{1} y_{1}^{1}+ \\ &\quad \boldsymbol{c}_{2}^{-2} y_{2}^{-2}+\boldsymbol{c}_{2}^{-1} y_{2}^{-1}+\boldsymbol{c}_{2}^{0} y_{2}^{0}+\boldsymbol{c}_{2}^{1} y_{2}^{1}+\boldsymbol{c}_{2}^{2} y_{2}^{2}+ \\ &\quad \boldsymbol{c}_{3}^{-3} y_{3}^{-3}+\boldsymbol{c}_{3}^{-2} y_{3}^{-2}+\boldsymbol{c}_{3}^{-1} y_{3}^{-1}+\boldsymbol{c}_{3}^{0} y_{3}^{0}+\boldsymbol{c}_{3}^{1} y_{3}^{1}+\boldsymbol{c}_{3}^{2} y_{3}^{2}+\boldsymbol{c}_{3}^{3} y_{3}^{3} \end{aligned}\]\(y_{l}^{m}(\theta, \phi)\)为勒让德多项式，具体表达式如下。以相机位置作为球坐标系原点，给定要观察的高斯椭球后，根据相机位置和高斯椭球中心的连线便可以得到方位角
\[\begin{aligned} y_l^m(\theta, \varphi) &= \begin{cases} \sqrt{2} K_l^m \cos(m\varphi) P_l^m(\cos\theta) & m > 0 \\ \sqrt{2} K_l^m \sin(-m\varphi) P_l^{-m}(\cos\theta) & m < 0 \\ K_l^0 P_l^0(\cos\theta) & m = 0 \end{cases} \\ P_n(x) &= \frac{1}{2^n \cdot n!} \frac{\text{d}^n}{\text{d}x^n} \left[(x^2 - 1)^n\right] \\ P_l^m(x) &= (-1)^m (1 - x^2)^{\frac{m}{2}} \frac{\text{d}^m}{\text{d}x^m} \left(P_l(x)\right) \\ K_l^m &= \sqrt{\frac{(2l + 1)(l - |m|)!}{4\pi (l + |m|)!}} \end{aligned}\]勒让德多项式举例如下
\[\begin{aligned} y_{0}^{0}&=\sqrt{\frac{1}{4\pi}} = 0.28\\ y_{1}^{-1}&=-\sqrt{\frac{3}{4\pi}}\frac{y}{r}=- 0.49\times\frac{y}{r}\\ y_{1}^{0}&=\sqrt{\frac{3}{4\pi}}\frac{z}{r}=0.49\times\frac{z}{r} \end{aligned}\]光栅化
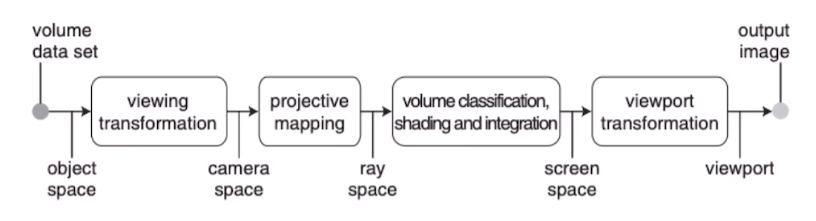
光栅化将每个3D高斯投影到2D屏幕上，并按深度顺序将其颜色和透明度累加到对应像素，生成最终图像。3D高斯椭球的投影具体来说可以细分为四个过程：观测变换、投影变换、视口变换、像素离散。
观测变换是从世界坐标系转换到相机坐标系的过程，本质上是仿射变换，通过乘相机外参矩阵实现。观测变换好比线性代数中基向量的变换，同一向量在不同基下的表达系数不同；同一物体在世界坐标系和相机坐标系中的表达也是不同的，观测变换就是两种坐标系之间的转换。
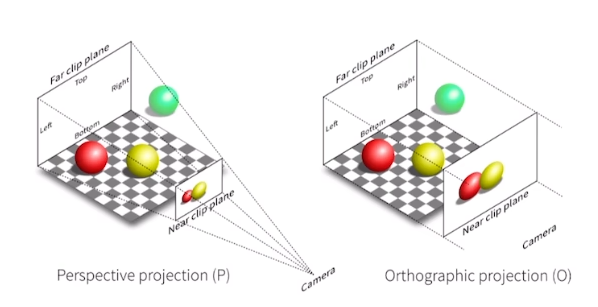
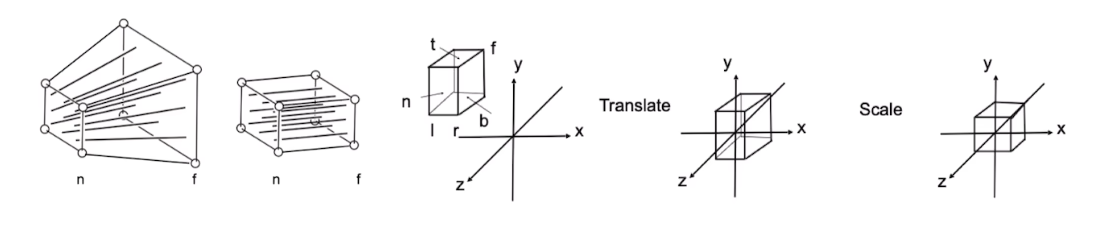
投影变换是从相机坐标系转换到图像平面的过程，又分为透视投影和正交投影。正交投影即忽略深度，不存在近大远小的效应。透视投影可以看作是先将视锥通过非线性变换化为正交投影相同的情况。两种投影都会先将要观察的空间变换到归一化坐标系（NDC），即\([-1, 1]^3\)范围内，然后正交投影忽略深度便转化到二维图像平面。
透视投影符合人眼成像规律，应用更广泛，变换示意图和相应的变换矩阵如下
要观察的视锥按如下方法确定：SfM中获得的内参矩阵中，fx和fy分别为水平焦距和竖直焦距，与图像的宽度和高低一起可以算出FOVx和FOVy，再根据指定的zfar和znear，便可以确定要投影的区域和相应的投影矩阵。
视口变换是将投影得到的归一化平面还原到符合图像长宽的图像坐标系过程，即将\([-1, 1]^2\)的矩形还原到\([0, w] \times [0, h]\)
变换矩阵为
\[\boldsymbol{M}_{\text{viewport}} = \begin{bmatrix} \frac{w}{2} & 0 & 0 & \frac{w}{2} \\ 0 & \frac{h}{2} & 0 & \frac{h}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]像素离散是将连续图像坐标系离散采样到像素坐标系的过程，根据像素中心点是否在图像中决定是否渲染该像素
高斯球参数在变换中传递
设世界坐标系下的高斯核中心为\(\boldsymbol{t}_k= [t_{0}, t_{1}, t_{2}]^{\top}\)，协方差矩阵为\(\boldsymbol{V}''_k\)，高斯核为\(r''(k)=G_{\boldsymbol{V}''_k}(\boldsymbol{t} - \boldsymbol{t}_k)\)；
相机坐标系下的高斯核中心为\(\boldsymbol{u}_k= [u_{0}, u_{1}, u_{2}]^{\top}\)，协方差矩阵为\(\boldsymbol{V}'_k\)，高斯核为\(r'(k)=G_{\boldsymbol{V}'_k}(\boldsymbol{u} - \boldsymbol{u}_k)\)；
归一化坐标系的高斯核中心为\(\boldsymbol{x}_k= [x_{0}, x_{1}, x_{2}]^{\top}\)，协方差矩阵为\(\boldsymbol{V}_k\)，高斯核为\(r(k)=G_{\boldsymbol{V}_k}(\boldsymbol{x} - \boldsymbol{x}_k)\)；
观测变换为\(\boldsymbol{u}=\boldsymbol{W}\boldsymbol{t} + \boldsymbol{d}\)，则\(\boldsymbol{u}_k = \boldsymbol{W}\boldsymbol{t}_k + \boldsymbol{d}，\boldsymbol{V}'_k = \boldsymbol{W}\boldsymbol{V}''_k\boldsymbol{W}^\top\)；
投影变换为\(\boldsymbol{x}=m(\boldsymbol{u})\)，雅可比矩阵为\(\boldsymbol{J}\)，则\(\boldsymbol{x}_k = m(\boldsymbol{u}_k)，\boldsymbol{V}_k = \boldsymbol{J}\boldsymbol{V}'_k\boldsymbol{J}^\top = \boldsymbol{J}\boldsymbol{W}\boldsymbol{V}''_k\boldsymbol{W}^\top\boldsymbol{J}^\top\)。
由于投影变换为非线性变换，而希望高斯椭球只进行线性的仿射变换（非线性变换不能准确传播协方差矩阵），对于均值这一个点可以直接应用非线性的投影变换，不存在形变的问题；而协方差则需要用雅可比矩阵在高斯核中心进行局部线性化，代替仿射变换矩阵\(\boldsymbol{W}\)。操作之后，均值在归一化坐标系中，后续再进行视口变换即可；而协方差在未缩放未平移的正交坐标系中，不需要作视口变换。
雅可比矩阵的具体计算方式如下：假设视锥中的点为\([x, y, z, 1]^\top\)（写成齐次形式），可以求出变换到正交坐标系中的对应坐标，由此可求得雅可比矩阵
\[\begin{aligned} \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & -nf \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} &= \begin{bmatrix} nx \\ ny \\ (n + f)z - nf \\ z \end{bmatrix} = \begin{bmatrix} \frac{nx}{z} \\ \frac{ny}{z} \\ (n + f)-\frac{nf}{z} \\ 1 \end{bmatrix} = \begin{bmatrix} f(x) \\ f(y) \\ f(z) \\ 1 \end{bmatrix}\\ \boldsymbol{J} &= \begin{bmatrix} \frac{\text{d}f(x)}{\text{d}x}&\frac{\text{d}f(x)}{\text{d}y}&\frac{\text{d}f(x)}{\text{d}z}\\ \frac{\text{d}f(y)}{\text{d}x}&\frac{\text{d}f(y)}{\text{d}y}&\frac{\text{d}f(y)}{\text{d}z}\\ \frac{\text{d}f(z)}{\text{d}x}&\frac{\text{d}f(z)}{\text{d}y}&\frac{\text{d}f(z)}{\text{d}z} \end{bmatrix} = \begin{bmatrix} \frac{n}{z}&0&-\frac{nx}{z^{2}}\\ 0&\frac{n}{z}&-\frac{ny}{z^{2}}\\ 0&0&\frac{n f}{z^{2}} \end{bmatrix} \end{aligned}\]图像合成
渲染过程中将图像拆分成\(16\times16\)的区块（tile），高斯椭球也随之被划分。GPU 为每个区块分配一个线程，区块之内共享内存。图像合成采用\(\alpha\)-blending 的方法，对于每一个区块，将高斯椭球按深度从近到远排序，由近到远遍历每个高斯椭球来填充像素的不透明度，直到该区块内所有像素的\(\alpha=1\)（完全不透明）为止；若混合完所有高斯椭球仍未达到\(\alpha=1\)则用背景颜色填充剩余不透明度。渲染过程中仍然执行以像素为单位的足迹渲染，但没有 NeRF 中从像素找粒子的过程。
前向渲染中，不透明度\(\alpha\)通过以下递推公式对图像产生作用，其中\(C_{acc}\)为之前累积混合得到的颜色，\(T_{acc}\)为之前累积的透射率（初始时\(T_0=1\)），\(C_{\text{final}}\)为当前这一层混合完成之后的颜色 \(\begin{aligned} \boldsymbol{C}_\text{final}&=\boldsymbol{C}_i\cdot\alpha_i+\boldsymbol{C}_\text{acc}\cdot(1 - \alpha_i)\\ T_\text{final}&=T_\text{acc}\cdot(1 - \alpha_i) \end{aligned}\) 推导出等价的通项公式如下 \(\begin{aligned} \hat{C}(r)&=\sum_{i = 1}^{N} T_i\alpha_i c_i\\ T_i&= \prod_{j = 1}^{i - 1} (1 - \alpha_j) \end{aligned}\) 在公式上，\(\alpha\)-blending 的方法和体渲染是一致的，但实现却完全不同。3DGS中的\(\alpha\)-blending是将离散的几个高斯椭球进行投影和颜色混合；而NeRF中的体渲染是沿光线进行密集采样并求和（将沿光线的连续积分离散化）。
补充知识
仿射变换
仿射变换是通过线性变换和平移来改变对象的位置和形状，保持原有对象的直线性和平移性，即二维图形之间的相对位置保持不变，平行线依然是平行线，且直线上的点的位置顺序不变的几何变换；可以实现平移、旋转、缩放和剪切等操作。另外，在进行多个仿射变换时，他们的顺序会影响最终结果。
仿射变换可以表示为乘以一个矩形（这个矩阵又可以分解为旋转矩阵和缩放矩阵）再加上一个向量的形式。为了方便表示连续的仿射变换，也可以用齐次形式表示
\[\begin{aligned} \boldsymbol{y} &= \boldsymbol{A} \cdot\boldsymbol{x} + \boldsymbol{b} = \boldsymbol{R}\boldsymbol{S}\cdot \boldsymbol{x} + \boldsymbol{b}\\ \begin{bmatrix} \boldsymbol{y} \\ 1 \end{bmatrix} &= \begin{bmatrix} \boldsymbol{A} & \boldsymbol{b} \\ \boldsymbol{0}^\top & 1 \end{bmatrix} \begin{bmatrix} \boldsymbol{x} \\ 1 \end{bmatrix} \end{aligned}\]体渲染公式
连续域中的公式为一个第一类曲线积分（此处省略推导），其中\(T(s)\)为在\(s\)之前，光线未被遮挡的概率；\(\sigma(s)\)为\(s\)处光线撞击粒子（被阻碍）的概率密度；\(C(s)\)为光线在\(s\)处造成的颜色；\(\hat{C}(s)\)为渲染得到的颜色
\[\begin{aligned} \hat{C}(s) &= \int_{0}^{+\infty} T(s) \sigma(s)C(s) \text{d}s \\ T(s) &= e^{-\int_{0}^{s} \sigma(t) dt} \end{aligned}\]离散域的公式如下（此处省略推导），将光线\([0, s]\)划分为\(N\)个等距区间\([T_n\to T_{n+1}], n=0,1,\cdots,N\)，区间间隔长度\(\delta_n\)，区间足够小，认为区间内概率密度\(\sigma_n\)和颜色\(c_n\)固定
\[\begin{aligned} \hat{C}(r)&=\sum_{i = 1}^{N} T_i\alpha_i c_i\\ \alpha_i &=1 - \text{e}^{-\sigma_i\delta_i}\\ T_i&=\text{e}^{-\sum_{j = 1}^{i - 1}\sigma_j\delta_j}= \prod_{j = 1}^{i - 1} (1 - \alpha_j) \end{aligned}\]运动恢复结构
运动恢复结构（Structure from Motion，简称SfM）是通过三维场景的多张图象恢复出该场景的三维结构信息以及每张图片对应的摄像机参数的方法。三种典型的运动恢复结构任务分别为：欧式结构恢复（摄像机内参数已知，外参数未知）、仿射结构恢复（摄像机为仿射相机，内、外参数均未知）和透视结构恢复（摄像机为透视相机，内、外参数均未知）
该问题可以建模为：已知\(n\)个三维点\(\boldsymbol{X}_j\)在\(m\)张图像中的对应的像素坐标\(\boldsymbol{x}_{ij}\)，\(\boldsymbol{M}_i、\boldsymbol{K}_i、[\boldsymbol{R}_i~ \boldsymbol{T}_i]\)分别为相机的投影矩阵、内参矩阵和外参矩阵，满足 \(\boldsymbol{x}_{ij}=\boldsymbol{M}_i\boldsymbol{X}_j = \boldsymbol{K}_i[\boldsymbol{R}_i~ \boldsymbol{T}_i]\boldsymbol{X}_j\quad i = 1,\dots,m;~j = 1,\dots,n\) 需要求解\(m\)个投影矩阵\(\boldsymbol{M}_i\)和\(n\)个三维点坐标\(\boldsymbol{X}_j\)