FPGA和ASIC的共同地基

《高等数字集成电路分析与设计》课程梳理

发表于 2026/01/29 更新于 2026/01/30

AMD EPYC 9004服务器处理器

作者 Hatrix

52 分钟阅读

FPGA和ASIC的共同地基

二进制编码

数字信号是离散信号的数字化表示，其变化量是最小量的整数倍，表示方法是二值逻辑/二进制。计算机使用二进制表示信息，这些二进制数就是所谓的代码，给每一组代码赋予一定的含义就是编码。编码有有权码和无权码之分，常见的有权码有 8421 码、5421 码、2421 码等，无权码有余三码、余三循环码、格雷码等。二进制在物理实现上用高低电平两种状态进行表示，电信号的状态易于区分、抗干扰能力较强。二值逻辑在实现上需要对逻辑电平的标准有统一的规定，即高电平和低电平的电压范围，常用的标准有 TTL、CMOS、RS232。不同标准对高低电平的定义不尽相同，使用不同逻辑电平标准的器件时，就需要电平转换芯片充当翻译的角色，使信息能够被准确传递。

相较于十进制，二进制在表示同样的数时需要更多的位数，用加权的方式，可以在不同数制之间互相转化。二进制只是一种十进制以外的数制，其运算规则与十进制无异。一个数叫一位，8 位叫一个字节；二进制中，1kb 为 1024 byte。大部分计算机用第一位表示正负，剩下位数表示数字。在机器中使用的连同符号一起数码化的二进制数称为机器数，机器数对应的真正数值称为真值。8 位机器数表示的真值范围为 0-255，16 位真值表示的真值范围为 0-65535。

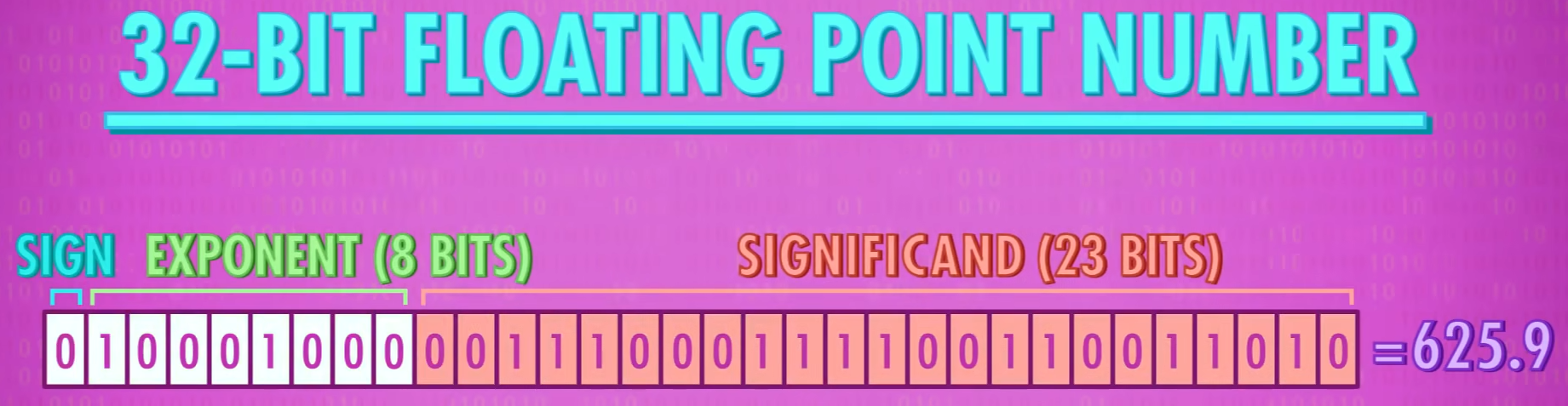
数据可用科学计数法表示，根据小数点的位置是否固定分为定点数和浮点数。浮点数表示法中以一定的位宽分别表示符号、阶数和尾数，阶数的位宽决定可以表示数据的范围，尾数的位决定可以表示数据的精度。为了解决编码空间浪费的问题，一般规定尾数的第一位为 1，以 0.1xxx 的形式表示，这一过程称为归一化；为了使阶数可以表示负指数，给阶数部分加上一个根据位宽而定的居中的数作为偏置，负指数加上偏置后变为正指数。IEEE-754 为国际通用的浮点数标准。

文字按照一定的编码方式对应为一串二进制数，因此也可由几位二进制数表示。ASCII 用 7 位二进制数表示字母，数字，标符号和特殊命令符号。而对于中文和日文这样有成千上万个字符的语言，各国有不同的多字节编码方案，但互不兼容。为此诞生了 Unicode，统一了所有的编码标准，最常见的 Unicode 是 16 位的。音频是时间上的一维信号，图片/颜色是二维的矩阵或者张量信号，视频则是由一帧帧图片构成，这些信息均可以由二进制编码。

布尔代数及实现

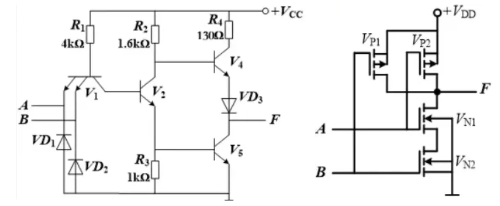
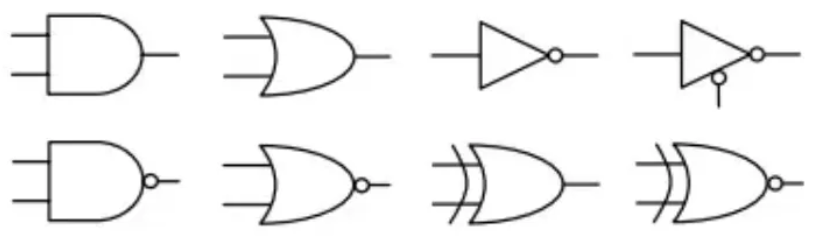
布尔代数是专门研究二值逻辑的数学结构，真值表是其中的重要工具，用于列举逻辑表达式(逻辑函数)在所有可能输入情况下的结果。在设计逻辑电路的过程中，需要对逻辑函数进行化简，可以使用公式、卡诺图、QM 法等方法完成操作，常见公式和方法具体步骤的资料丰富，此处省略。布尔代数定义了与、或、非、与非、或非、异或、同或七种基本运算。基本运算叠加复合，可以构成许多实用的逻辑函数。有了逻辑函数的概念后，还需要用电路去实现，以 TTL 和 CMOS 与非门为例，内部结构分别如下

利用二极管、三极管、场效应管等晶体管，可以构成全部七种能完成基本运算的逻辑门，实际使用时都是封装好的成熟芯片，故一般无需掌握其内部结构，但对芯片数据手册中的常用参数(阈值电压、噪声容限、扇出系数、传输延迟时间、动态尖峰电流等)需要了解含义以便选型。除了七种基本逻辑运算，OC/OD 门和三态门也是常用的两种逻辑门，OC/OD 门的逻辑功能和普通逻辑门相同，但内部结构有所不同，用于配合上拉电阻用于实现线与的逻辑(线与多根信号线连在一起，一根信号线输出低电平则整个输出低电平)，其电路符号和普通逻辑门相同。三态门用于实现信号的分时复用，三态即除了高低电平外还有高阻态，高阻态是一种特殊的 “断开” 状态，此时接口在电气上与外部电路几乎隔离，不影响其他电路的工作，通常用于避免总线上的数据冲突。

组合逻辑

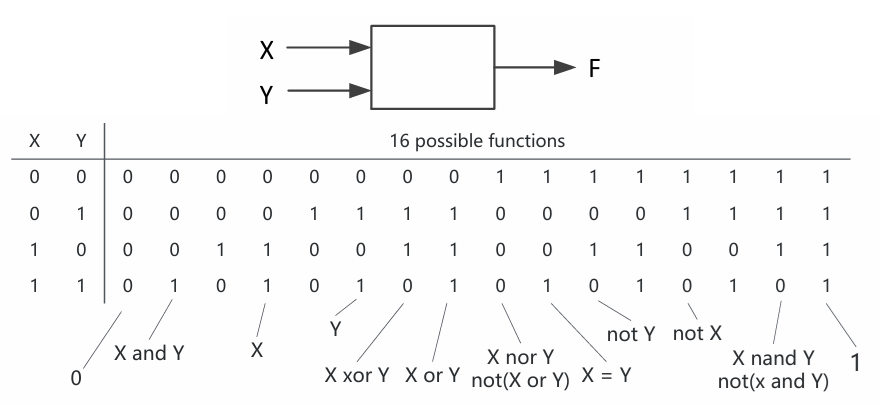
组合逻辑电路由逻辑门构成，任意时刻的输出仅取决于该时刻的输入，无反馈环节或记忆能力，功能可以完全分解成布尔表达式描述。以二输入的组合逻辑函数，穷举出来共有十六种，在 FPGA 中可以将所有十六种函数通过类似开关的机制做成一个叫做查找表 LUT （二输入查找表）的基本结构里。

对于较复杂的逻辑函数，同一个函数存在不同的实现方式，不同实现方式的实现面积和关键路径延时可能有所差别。实现面积即电路用晶体管实现后在芯片上占用的面积，面积在芯片设计中被视为一种重要的资源，关系到芯片的散热、集成的规模等等。关键路径指逻辑电路中信号传递经过的最长路径的耗时，包括导线延时和逻辑延时，逻辑延时即逻辑门 CMOS 充电到目标电平需要的时间。从输入到输出经过的逻辑门的串联层数称为逻辑级数，是组合逻辑深度的衡量。较少的逻辑级数通常可以降低信号传输延时。减少逻辑级数，本质是用复杂的单级门替代简单的多级门，单级门的晶体管数量（门级开销）会有所增加。实现面积和逻辑门延时往往是一对矛盾的指标，需要设计者在面积和速度之间进行权衡。

设计组合逻辑电路的大致思路为：确定输入输出，列出真值表，化简逻辑函数，用逻辑门实现。常用的逻辑功能基本都有封装好的成熟芯片，用 Verilog 也可以很方便地搭建且可以自己定制实现方式，可使用这些组件进行更高层次的设计，比如级联或构成功能丰富的系统。

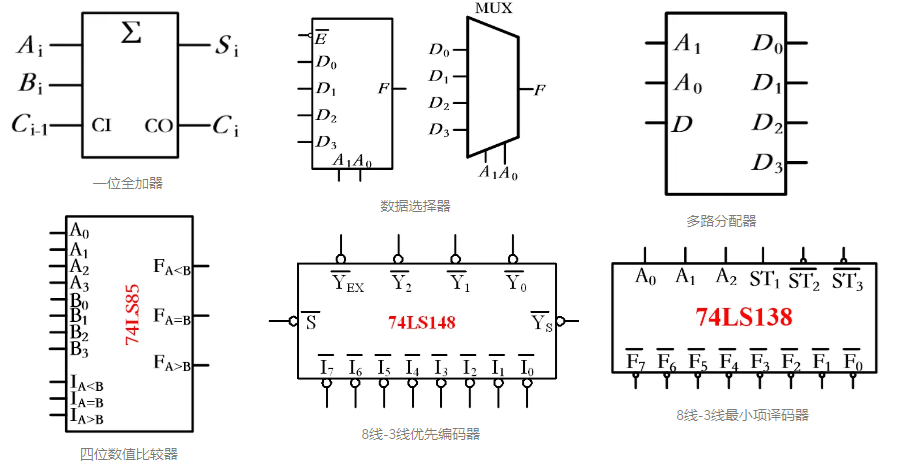
常用的逻辑电路模块举例如下

全加器：一位二进制数的加法，考虑进位；可级联成多位的加法器；配合补码的概念也可实现减法
数据选择器：在多个输入信号中选择一个传输到输出；可级联扩大选择范围
多路分配器：将一个输入信号选择传输到多个输出中的一个；可级联扩大选择范围
数值比较器：比较两个相同位数的二进制数的大小，可用于标志位的产生；可级联增加比较的位数
编码器：将一组二进制代码赋予特定的含义(如表示为对应的十进制数)；可级联增加支持的线数
仲裁器：优先编码器的一种
译码器：输入二进制代码，输出还原之后的特定输出信号；可级联增加支持的线数；将输出信号接到发光二极管上，就是所谓的显示译码器；当每个输出都是输入变量的最小项时，又称为最小项译码器。最小项译码器可以实现当前输入个数下的任意逻辑函数

组合逻辑中的竞争和冒险：在组合逻辑电路中，不同路径的输入信号变化传输到同一点门级电路时，在时间上有先有后，这种先后所形成的时间差称为竞争(Competition)。由于竞争的存在，输出信号需要经过一段时间才能达到期望状态，过渡时间内可能产生瞬间的错误输出，例如尖峰脉冲。这种现象被称为冒险(Hazard)。竞争不一定有冒险，但冒险一定会有竞争。

时序逻辑

时序逻辑电路由逻辑门和存储器构成，输出与之前输出状态有关，有反馈环节和记忆能力。时序逻辑电路接收信号之前的状态称为初态/原态，用 $Q^n$ 表示，接收信号之后建立的新稳态称为次态/新态，用 $Q^{n+1}$ 表示。所谓有记忆能力，就是指次态同时由输入和初态决定。相较于组合逻辑电路的输入而言，时序逻辑电路更重要的往往是时钟信号/触发信号的输入。复杂系统中，往往用时钟信号/触发信号来保证各个信号的动作在时间上同步。时序逻辑电路的表示方式有时钟方程+驱动方程+输出方程+状态方程，状态转换图，次态卡诺图等。

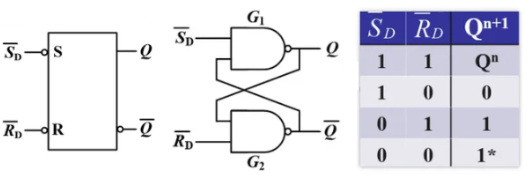
存储器的基本单元是触发器(Flip-Flop，简称 FF)，基本 RS 触发器也叫锁存器(latch)，其基本结构和真值表如下，通过改变输入信号，可以实现对状态 Q 的存储、置位和复位。锁存器可用于实现门控时钟，一般用于低功耗设计中，可有效消除毛刺，但初学者不建议使用。

触发器可以存储一位的信息，将它们并排使用便可以存储更多位数的信息，比如存储八位信息的寄存器、移位寄存器等更复杂的存储结构。触发器按逻辑函数实现的功能又细分为 RS 触发器、JK 触发器、D 触发器、T 触发器、T'触发器；按结构又细分为基本型触发器、同步型触发器、主从型触发器、边沿型触发器。触发器有电平触发和边沿触发，狭义上的触发器指边沿触发，而电平触发的叫锁存器。寄存器的基本组成单元为触发器/锁存器。而缓冲器与三者不同，没有数据保存的功能而更像是一个开关，主要用于隔离和增强信号的驱动能力。Verilog 设计中用到的触发器一般指边沿触发的 D 触发器。

时序逻辑中最常用的结构是计数器，由触发器和逻辑门构成。触发器之间采用不同的连接方式，可以跳过某些计数值从而实现任意进制的计数器、环形计数器、扭环形计数器等多种衍生功能。

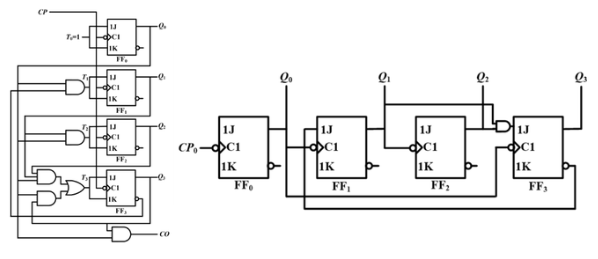
计数器分为同步计数器和异步计数器，同步计数器所有位的触发器均受时钟信号约束，工作频率高、传输延迟短、结构复杂；而异步计数器低位输出直接控制高位输入，结构简单，存在竞争和冒险产生的尖峰脉冲。下图左侧为同步计数器结构，右侧为异步计数器结构。

有限状态机 FSM 是时序逻辑中应用最广泛的模型。状态机推荐都写成三段式，逻辑清晰方便调试，一个时序 always 块用于描述当前状态，一个组合 always 块用于描述状态转移，一个时序或组合 always 块用于描述输出。下面是一个例子（为了聚焦于状态机模板本身，删掉了实际的功能，所以从功能上看起来只向外发起了一个 rd_req）

  
module read_cam
(
	input clk,
	input rstn,
	input in_ready,
	input in_valid,
	input rd_global_done,
	output reg rd_req
);
	localparam IDLE  = 3'd0;
    localparam CAM_0 = 3'd1;
    localparam CAM_1 = 3'd2;
    localparam CAM_2 = 3'd3;
    localparam CAM_3 = 3'd4;
    localparam CAM_4 = 3'd5;
    localparam DONE  = 3'd6;
	reg[2:0] state_cur, state_next;
    // 描述当前状态
	always @ (posedge clk) begin
		if (!rstn) begin
			state_cur <= IDLE;
		end
		else begin
			state_cur <= state_next;
		end
	end

    // 描述状态转移
	always @ (*) begin
		state_next <= state_cur;
		case (state_cur)
			IDLE:  if (in_ready) state_next <= CAM_0;
            CAM_0: if (in_valid) state_next <= CAM_1;
            CAM_1: if (in_valid) state_next <= CAM_2;
            CAM_2: if (in_valid) state_next <= CAM_3;
            CAM_3: if (in_valid) state_next <= CAM_4;
            CAM_4: if (in_valid) state_next <= DONE;
            DONE:  if (rd_global_done) state_next <= DONE;
			default: state_next <= IDLE;
		endcase
	end

    // 描述输出
	always @ (posedge clk) begin
		if (!rstn) begin
			rd_req <= 0;
		end
		else begin
            if ((state_cur == IDLE) && (in_ready)) begin
				rd_req <= 1;
			end
			else begin
				rd_req <= 0;
			end
		end
	end
endmodule

状态机有 Mealy 和 Moore 型之分，前者的状态机输出与当前状态和输入有关，在输入变化不同步的情况下可能引入时序问题，通常会实现成两段式；后者的状态机输出只和当前状态有关，通常实现成三段式。初学者建议一律实现成三段式的 Moore 型状态机。

算术逻辑

算术逻辑是组合逻辑中最重要的一类功能，例如加法器、乘法器和浮点预算等。计算机的整数运算系统中，数字一律被编码为二进制的补码。正数的补码和原码一致，负数的补码为原码按位取反再加一。下面对加法器、乘法器以及浮点运算的几种常见形式做一个概览介绍，具体实现见参考资料。

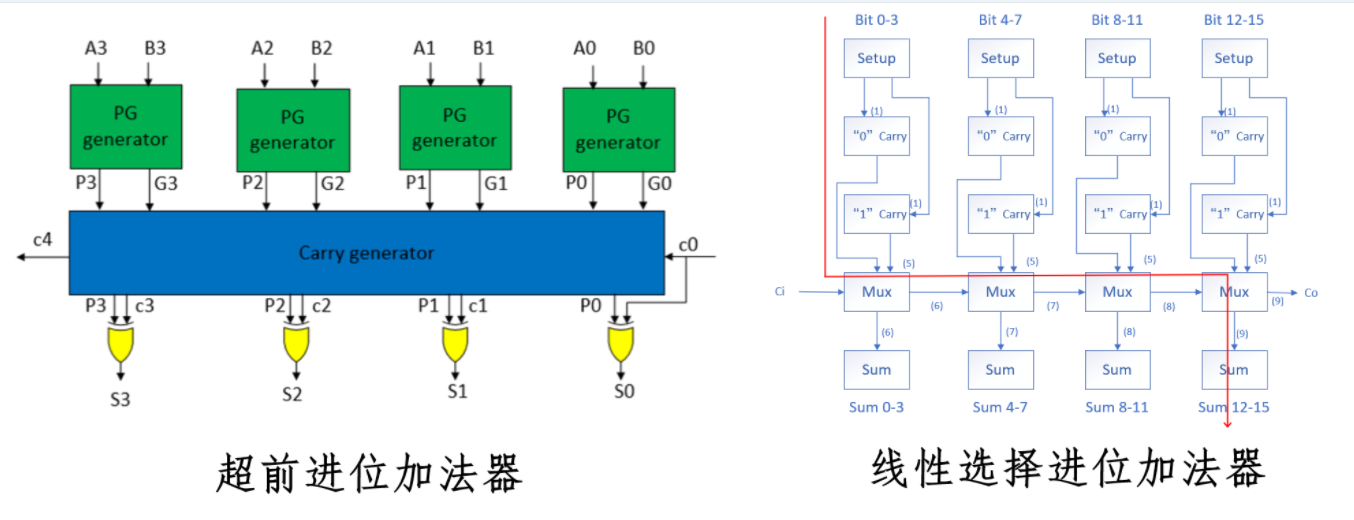
加法器的基本元件为半加器和全加器，由它们可构成行波进位加法器（串行进位加法器）、超前进位加法器、线性进位选择加法器等不同的加法器结构。相较于串行进位，后两者优化的关键在于并行地提前计算各位的进位，消除了高低进位之间的依赖关系，用面积换速度。此外还有通常以阵列形式使用的进位保留加法器。

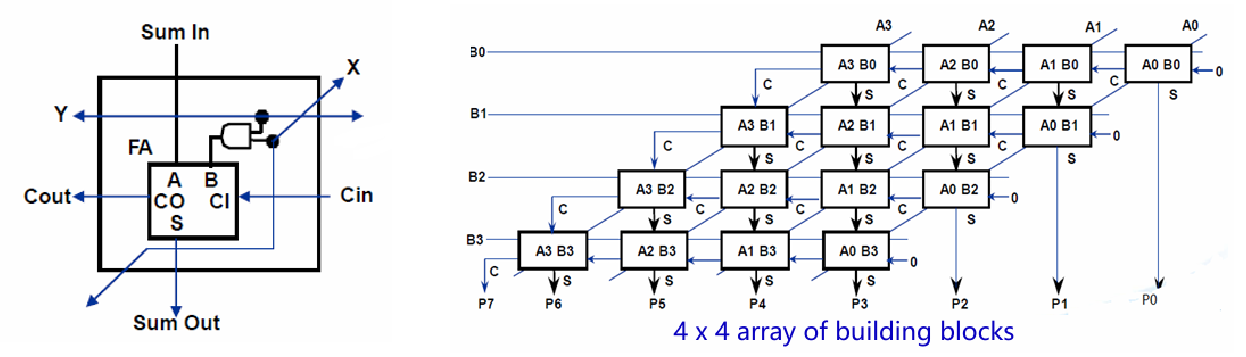
二进制乘法的本质是计算部分积累加，优化的关键也在于减少部分积求和的次数。阵列乘法器是一种常用的实现方式，由半加器、全加器和与门构成。此外还有加入一定时序逻辑的顺序乘法器、通过编码来减少部分积次数的 Booth 乘法器、部分积压缩网络 Wallance Tree 等。

浮点数的运行普遍会比定点数复杂，所以一般先对数据作定点化，以定点化的形式完成处理后再转为浮点数。计算机的位宽是有限的，而实数域是无限的，当浮点运算结果超过尾数能表达的位宽时，一定会产生误差，位宽越大，误差越小。此时需要对数据进行舍入，最简单的舍入方式是直接舍掉多余的位，但一般误差较大。此外还有就近舍入，原理与十进制的四舍五入完全相同，将数据根据小数部分的值不同，向临近整数舍入。浮点数的加法需要统一阶数、尾数相加、最后归一化结果；浮点数的乘法需要指数相加、尾数相乘、归一化结果。

片上存储器

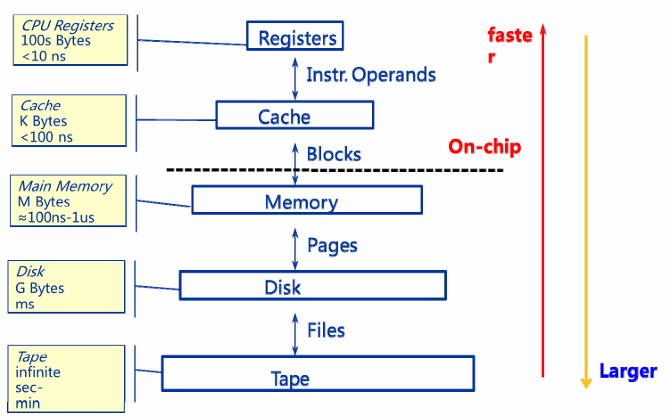
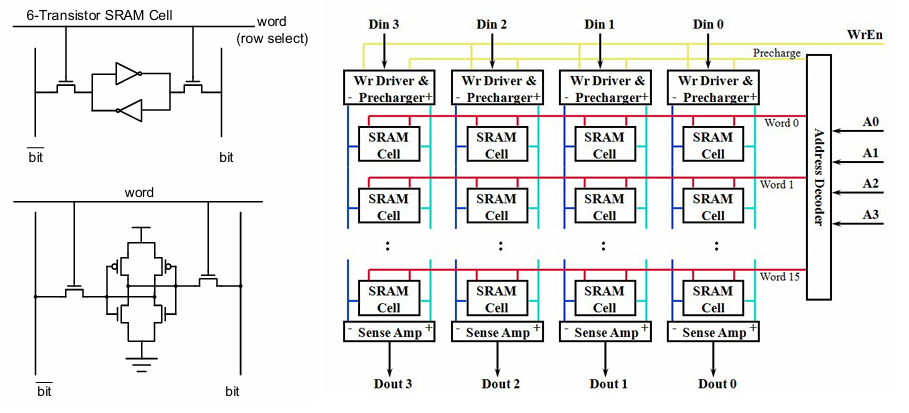
根据数据访问的局部性原理，现代计算机的存储系统设计呈现明显的层级结构，片上存储器属于离 CPU 最近的部分，容量小读写快，有寄存器堆和 SRAM 两种形式。

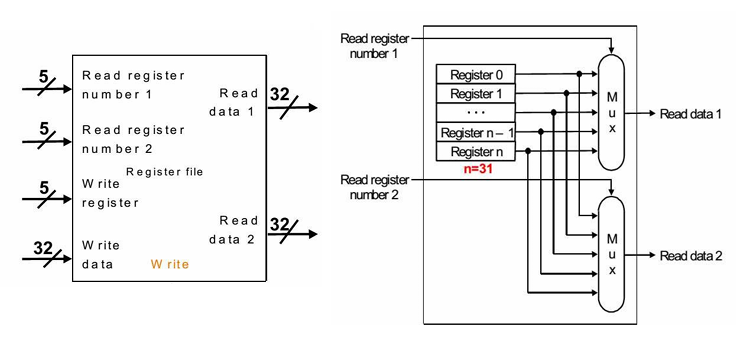
寄存器堆即多个寄存器构成的阵列，可以基于分离触发器的排列组合，可多个端口同时读写，用于 CPU 中的通用寄存器；也可以基于快速 SRAM 架构，一般只能两个端口读写，用于芯片上的数据快速存储。寄存器堆在实际实现时需要考虑扇入扇出的负载与速度之间的平衡，堆中的寄存器越多，扇入扇出负载越大，速度越慢；还需要注意读写口的数量直接影响寄存器堆的复杂度和规模。为保证访问速度，寄存器堆一般实现成小规模。

SRAM 是结构规整、密度更高的存储器，是除了寄存器之外最快的存储介质，功耗和成本也相对高。通过小规模 SRAM 的组合，可构建交织存储器阵列，用于应对大量数据的并行乱序随机访问。

时钟和时序

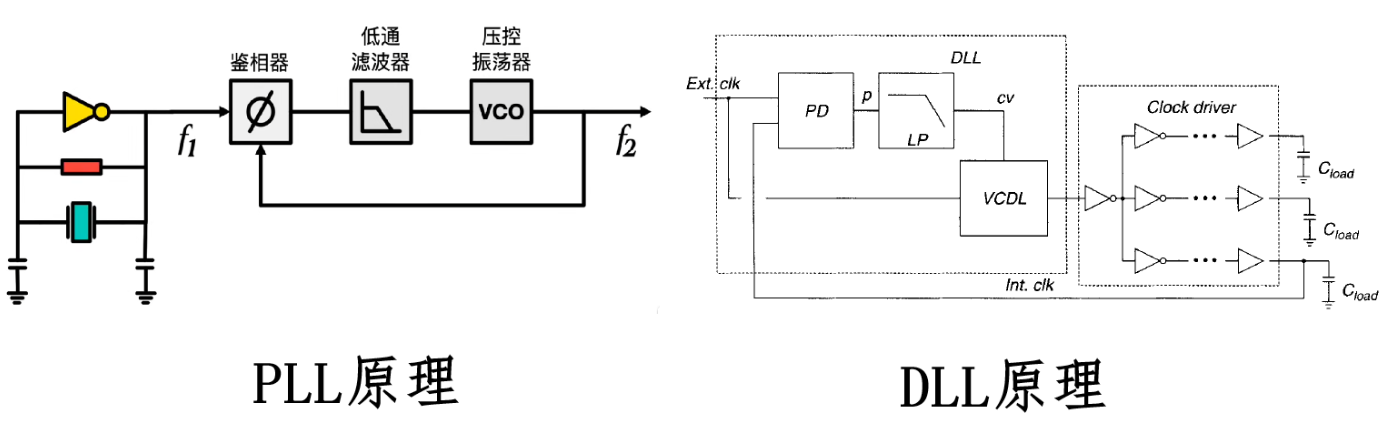
时钟信号最重要的参数包括频率/周期、占空比、上升/下降时间、时钟抖动等，在实现上会使用专门的振荡器或晶振产生固定频率的方波信号。基本的时钟控制包括锁相环 PLL 和延迟锁相环 DLL。PLL 通过闭环控制电压，由压控振荡器将输出频率锁定为参考频率的 (N/R) 倍，实现频率合成与相位同步，用于频率合成，有相位积累误差；DLL 用可控延迟线作反馈将时钟相位对齐，用于相位调节，可用作多相时钟或将不同时钟相位对齐。

门控时钟是 ASIC 设计中用于降低芯片功耗的常见方式，即控制时钟使能，让某一部分寄存器在不需要工作时不再翻转，可以显著降低动态功耗；具体方式上有 Latch 门控、触发器门控、可测性门控等。不过初学者不建议采用门控时钟设计。另外，时钟最好不要通过任何组合电路，也不要用组合电路产生时钟；另外，应尽量减少时钟的数目。

下面介绍一些概念。

同步时钟和异步时钟：时钟有同步时钟和异步时钟之分，同步时钟是指时钟源相同，频率相位有一定关系的时钟；否则为异步时钟。时钟源不同，则频率和相位没有任何关系；因为自然界没有任何两个完全相同的晶振，因此不同源时钟的频率和相位没有任何关系。

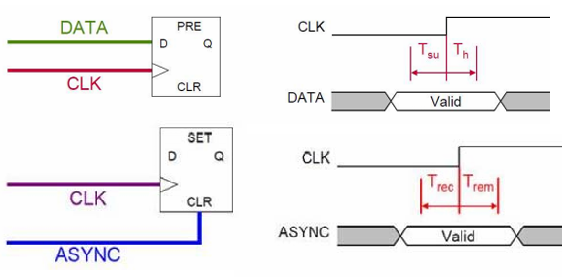
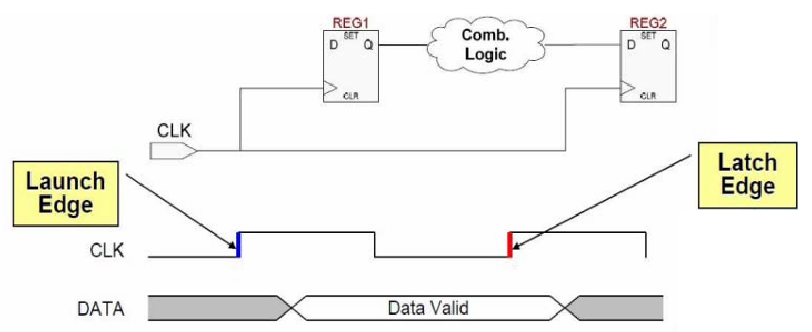
建立时间和保持时间：建立时间是指时钟上升沿到来之前，数据必须保持稳定的时间；保持时间是指时钟上升沿到来之后，数据必须保持稳定的时间。保存时间的意义在于源寄存器的输出不能太快到达目标寄存器，以防止新数据冲掉原来的数据。保持时间是对当前时钟沿而不是下一个时钟沿的约束。由于数据在时钟的上升沿被锁存，因此数据需要在时钟的上升沿的建立时间和保持时间内稳定不变。建立时间和保持时间由器件特性决定，在完成芯片选型后就随之确定。Xilinx FPGA 的建立时间和保持时间分别在 0.04ns 和 0.2ns 的量级，不同器件略有差异，具体可查阅器件的 DC and AC Switching Characteristics。对于异步信号，建立时间和保持时间的概念被称为恢复时间和移除时间。

建立时间关系和保持时间关系：建立时间关系是指当前数据从源寄存器的时钟启动沿到达目的寄存器的时钟锁存沿所用的这段时间，满足当前数据被锁存的建立时间。保持时间关系是指当前数据从源寄存器的时钟启动沿到达目的寄存器的时钟锁存沿所用的这段时间，满足上一个数据被锁存的建立时间。

启动沿和锁存沿：启动沿指传输到源寄存器的时钟沿，锁存沿指传输到目标寄存器的时钟沿。从时间上看，启动沿比锁存沿早一个时钟周期。实际上，启动沿和锁存沿是同一个时钟周期由时钟沿传输来的时钟信号。

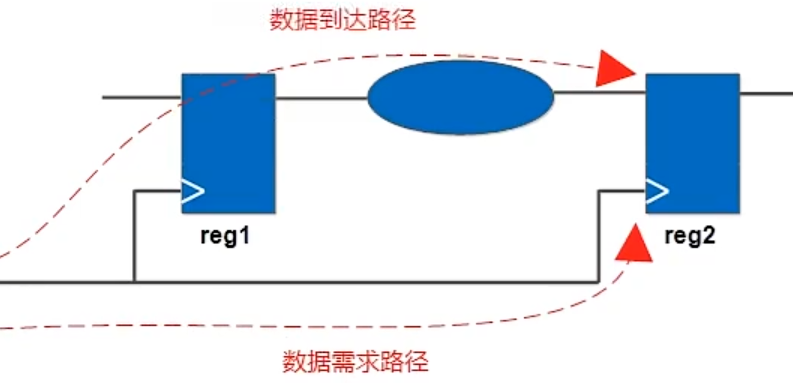
数据到达路径和数据需求路径：数据到达路径是指数据在两个寄存器间传输的实际路径，由此可推算出数据在两个寄存器间传输的实际时间。数据到达路径的起点是时钟沿，经过源寄存器的时钟输入端口、源寄存器的数据输出端口，最终到达目的寄存器的输入端口。数据需求路径是指为了确保稳定可靠且有效的传输（即满足相应的建立时间和保持时间要求），数据在两个寄存器之间传输的理论所需时间的计算路径。数据需求路径的起点也是时钟源，终点是目的寄存器的时钟输入端口。

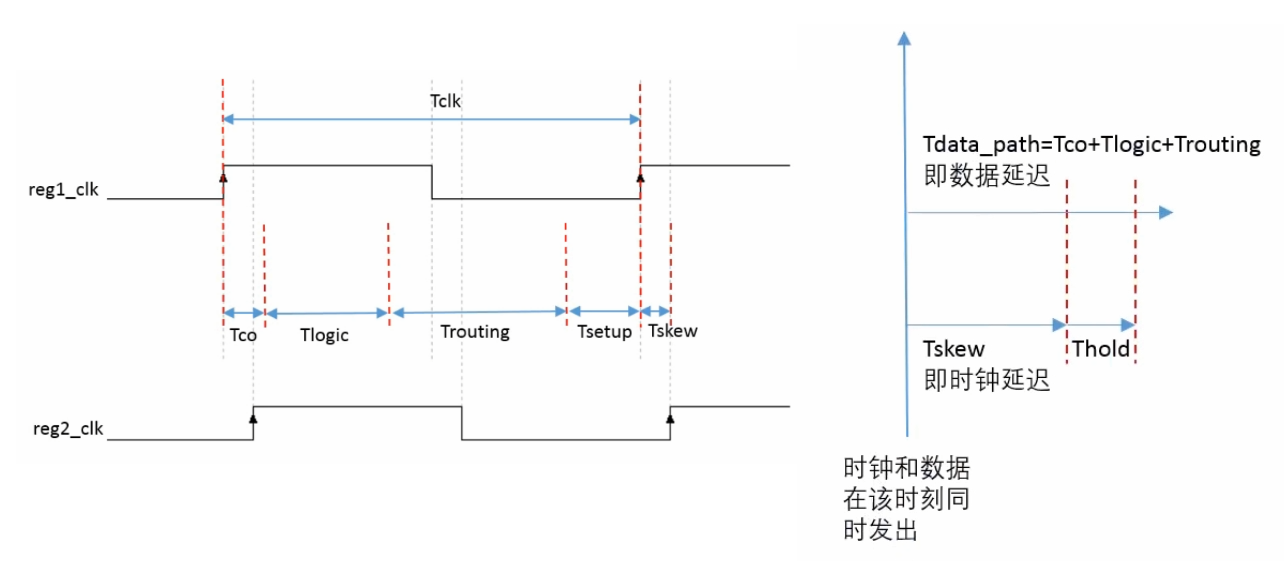
时钟模型要求的两个公式如下

\[\begin{aligned} &T_{\text{clk}} \geqslant T_{\text{co}} + T_{\text{logic}} + T_{\text{routing}} + T_{\text{setup}} - T_{\text{skew}}\\ &T_{\text{co}} + T_{\text{logic}} + T_{\text{routing}} \geqslant T_{\text{h}} + T_{\text{skew}} \end{aligned}\]

其中 $T_{\text{clk}}$ 为系统所能达到的最小时钟周期，$T_{\text{co}}$ 为源寄存器时钟到输出的时间，$T_{\text{logic}}$ 为组合逻辑延迟，$T_{\text{routing}}$ 为两级寄存器之间的布线延迟，$T_{\text{su}}$ 为建立时间，$T_{\text{h}}$ 为保持时间，$T_{\text{skew}}$ 为时钟倾斜。$T_{\text{co}}$、$T_{\text{su}}$、$T_{\text{h}}$ 都取决于芯片工艺，在芯片型号选定后就确定了，因此确定芯片后，只能通过 $T_{\text{logic}}$ 和 $T_{\text{routing}}$ 来改善 $T_{\text{clk}}$。其中 $T_{\text{logic}}$ 取决于 RTL 代码设计，$T_{\text{routing}}$ 取决于布局布线策略。$T_{\text{skew}}$ 在 FPGA 的同步时钟设计中一般忽略，因为 FPGA 中的时钟树会尽量保证到达每个寄存器的延迟相同。

时序约束

待梳理

多时钟系统

许多系统需要在设计中采用多时钟，不同时钟之间要求一定的建立和保持时间，需要引入附加的时序约束条件，要求将某些异步信号同步化。若系统中存在异步时钟域之间的信号传输，电路就会出现亚稳态；事实上，只要相位差不固定，直接采样就可能存在亚稳态问题。

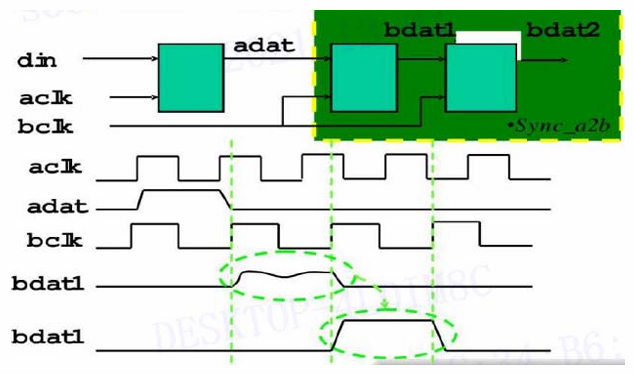
在许多应用中，只将异步信号同步化还不够，当系统中有两个及以上非同源时钟时，数据的建立和保持时间很难得到保证，此时最好的办法是将所有的非同源时钟同步化，实现上是使用带使能端的 D 触发器，并引入一个高频时钟来实现信号的同步化。使用两级 D 触发器是跨时钟域同步的经典方案，第一级捕获异步信号，第二级滤除亚稳态。末尾的 D 触发器为数据输出控制。

跨时钟域数据同步常使用 Dual Port RAM 和 FIFO 作为缓冲桥梁，上游时钟控制写入，下游时钟控制读取；FIFO 使用时注意 FIFO 深度设置和 FIFO 门限控制。异步时钟设计时，还应该尽量减少握手控制信号的数目，以避免同步化造成的信号拉伸而破坏信号之间的相位关系。快时钟域信号进入慢时钟域时，要注意信号丢失的避免和检测。双边可读写RAM对两边端口的时钟相位有严格的时序要求，否则极易出现读写冲突。

在跨时钟域时序分析中，当两个时钟之间没有确定的相位关系时，约束两者之间的时序关系是没有意义的，针对这种情况，只能采用标准的跨时钟域处理数据，还要记得设置两者之间的时序路径为 false_path。

并行技术

这里介绍空间并行和流水线并行两种并行技术。

空间并行实质上就是用面积换速度，通过多个完全相同的并行处理单元来提高系统性能，典型应用比如 ping-pong 操作。在中间组合逻辑的运算所需时间超过一个时钟周期，且逻辑不易分割时，也可以采用这种技术来减少大运算逻辑对系统速率的影响，根据需要复制一个或多个本体逻辑并用 Mux 选择输出，本质上是让其它所需时间小于一个时钟周期的步骤多处理一些数据来填满运算缺口，消除 bubble。

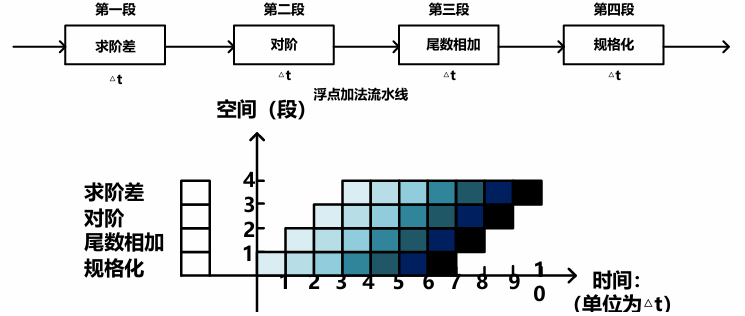
下面重点介绍流水线并行技术。流水线技术的思想非常朴素，将一个重复的时序过程分解为若干个子过程，每个子过程都可有效地在其专用功能段上与其它子过程同时执行。每个子过程称为流水线的“级”或“段”，由专用的功能段实现，段的数目称为流水线的深度。

流水线需要等待第一个任务流出之后，流水过程才进入稳定工作状态，每一拍流出一个结果。各个功能段所需时间应尽量相等（这个时间通常为一个时钟周期，称为一拍），否则时间长的段会成为瓶颈，造成流水线堵塞或断流。流水线适合大量重复的时序工作，只有输入端能连续地提供任务，才能充分发挥流水线的效率。

流水线性能的常用量化指标如下，T 为时钟周期

最大吞吐量：若每个时钟周期能从流水线输出一个结果，则最大吞吐量为 $f=\frac{1}{T}$
加速比：一条 K 段流水线处理 n 个任务，花费总时间为 $T_k = [K+(n-1)]T$，加速比为 K 段流水线对等效非流水线的加速因子 $S_k = \frac{T_1}{T_k} = \frac{nKT}{[K+(n-1)]T} = \frac{nK}{K+n-1}$
流水线频率：$E_k = \frac{S_k}{K} = \frac{n}{K+n-1}$，$n\to \infty$ 时效率接近 1
吞吐率：单位时间执行的操作数，$H_k=\frac{n}{[K+(n-1)]T} = \frac{nf}{K+(n-1)}$，$n\to \infty$ 时得到最大吞吐率

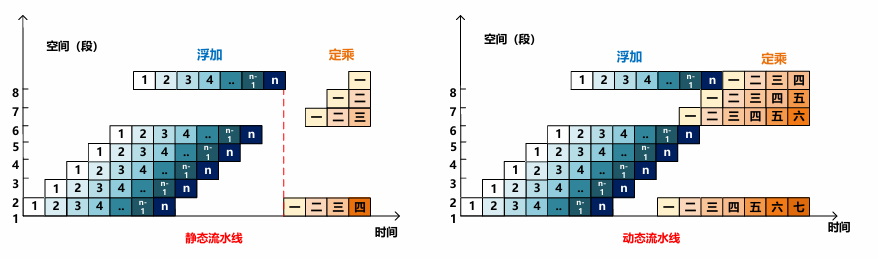
流水线的工作过程可用时空图来描述，横坐标代表时间，纵坐标代表流水线的各个段。

流水线分静态流水线和动态流水线，前者用来实现确定的功能，只有当输入是一串相同的运算操作时，才能充分发挥效率；后者除了流水线连接外还允许前馈和反馈连接，又称非线性流水线，可处理非相同运算的一串操作，控制更加复杂。

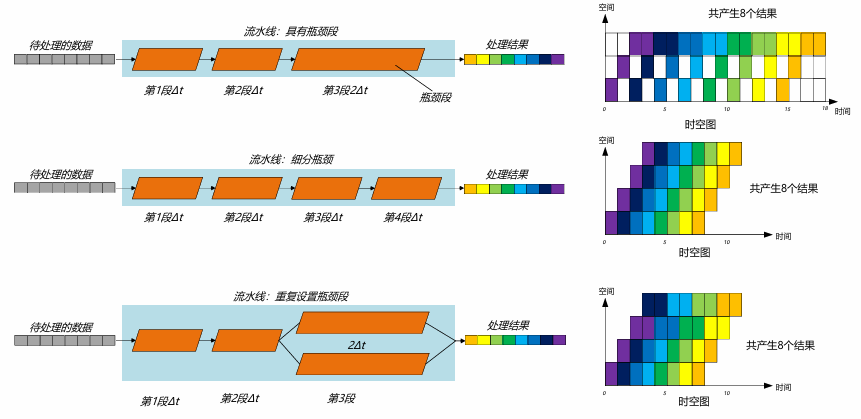
对于具有瓶颈段的流水线，可采用细分瓶颈或重复设置瓶颈段的方式来提高效率。

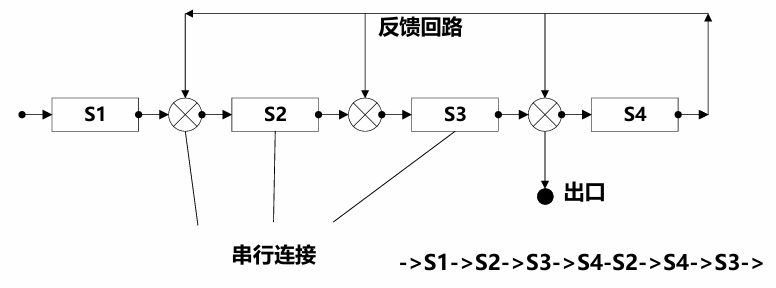
非线性流水线举例如下，由于存在反馈，流水线中存在冲突的可能，因此一个重要的问题是确定什么时候向流水线引入新的输入才能使得输入的数据和先前操作的反馈数据在流水线中不冲突，也就是所谓的流水线调度问题。非线性流水线相关的内容后续更新，这里暂时略过。

线性流水线和非线性流水线都是硬件设计的概念，上升到更高的架构层次，流水方式有固定流水（硬件确定流水路径）和可变流水（软件确定流水路径）。

可重构设计技术

这部分常见的一些缩写包括：

RPU：Reconfigurable Processing Unit，可重构单元
RCA：Reconfigurable Cell Array，可重构单元阵列
PE：Processing Element，处理单元
RPEA：Reconfigurable Processing Element Array，可重构处理单元阵列

细粒度可重构器件最主流的就是 FPGA，粗粒度的包括 Matrix、REMARC、MorphoSys 等。预先配置的称为静态重构，实时配置的称为动态重构。

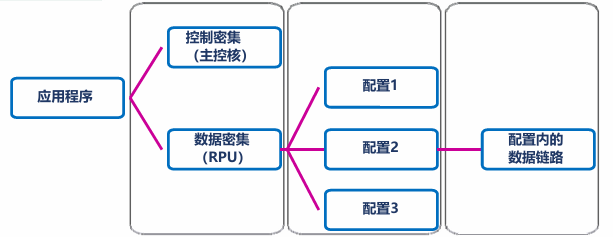
可重构硬件架构为混合架构，由主控核+可重构处理单元的阵列构成。RPU 的微架构上包括 Buffer、FIFO 等局部存储、集成 DMA，以及专门的控制器等。典型的架构有 Zippy、MorphoSys、ADRES、XPP 等。

可重构设计中研究的关键问题包括阵列设计、存储层次设计和控制流处理。

阵列设计

阵列设计需要考虑阵列规模、互联方式、流水方式等诸多参数，为了在有限的设计参数集中找到最优配置方案，提出了设计空间探索的概念。设计空间探索，简单来说就是在一堆可选的硬件架构方案里，用自动化方法找到 PPA（Performance、Power、Area）最优的那个方案。设计空间探索的目标就是评估并权衡 PPA 并找到满足约束的最优解，方法上会使用参数化建模，用高层模型（C/C++）描述算法和架构，定义架构的参数模板，生成架构描述文件，然后仿真遍历或搜索参数组合，快速评估不同方案。

存储层次设计

存储设计包括阵列内存储、阵列间存储和片外存储三个层次。

阵列内存储设计的目标是利用数据重用局部性，实现阵列内不同配置间较多临时数据的快速交换。一个重要的设计经验是用 FIFO 将 2D 数据拆成连续的 1D 流，按行或列顺序流式传输，规避 2D 随机访存，实现高速无冲突的流水线传输。
阵列间存储设计的目标是实现架构内所有阵列之间临时数据的高效传输。
片外存储设计的目标是实现架构与主控核之间的高效数据传输。

寄存器文件也会分层设计，寄存器文件指 PE 中用来存放正在使用的数据的一小块超快速存储。

局部寄存器文件 LRF：由硬件管理，用于缓存单个 PE 的计算结果。
分布式寄存器文件 DRF：由软件管理，以数据重用的方式实现少数几个 PE 之间的快速数据交换。
全局寄存器文件 GRF：由软件管理，利用数据访问的局部性原理，实现所有 PE 之间的数据交换。GRF 分配的方法有干涉图染色法、双缓冲策略等。

资源分配上，DRF 和 GRF 对 PE 而言都属于公共资源，需要合理调度才能提高效率，常见的方法包括：负载平移、模调度、干涉图染色法、双缓冲策略、线性扫描等。负载平移即让每个 DRF 的寄存器占用和访问压力更均衡。模调度是在循环流水线调度的同时分配 DRF，让计算调度和寄存器分配同步优化。干涉图染色法是图论中的算法，将变量作为顶点，寄存器（不能共用）作为边来构成干涉图。双缓冲即两组 GRF 交替工作，消除 GRF 访问的等待时间。线性扫描是根据变量的生命周期对寄存器文件分时复用，即给不同时使用的变量分配同一个寄存器文件。

控制流处理

控制流是程序执行的顺序与逻辑分支，决定 “先执行哪段代码、是否循环、是否跳转 / 分支”，核心是程序的执行路径。控制流是与数据流（数据的计算、传输，如加减乘除、数组运算）相对的概念，数据流是 “做什么计算”，控制流是 “按什么顺序做”。

传统的软硬件划分中，RPU 阵列只负责数据流运算，主控核只负责控制密集计算；这种划分的问题在于，主控核与 RPU 的通信代价高，且主控核加速比极低，容易成为系统的性能瓶颈。因此需要进行层次化的控制流处理，将控制流分层下放，主控核负责顶层控制，RPU 阵列承担中下层控制流，这样 PRU 的硬件设计部分会复杂些，但可以减少与主控核的交互，提升局部执行效率。

对于较长的分支，可以对分支分别生成独立配置，执行时根据状态寄存器中存储的条件结果，只加载其中一个配置，另一个配置不占用阵列资源。RPU 在设计时包含指令控制器，用于接收主控核下发的顶层控制指令、处理单条指令等，并根据指令对应配置控制器，再由可重构计算阵列分层执行，实现全层级的控制流处理。

将中下层的控制流映射为配置间分支或阵列内分支都可以，两者各有适用的范围，需要综合考虑分支长度、阵列规模、阵列利用率和处理速度。配置间分支适用于长分支，需要切换配置，利用率高但处理速度相对较低；阵列内分支适用于短分支，处理速度快但阵列利用率较低。

指令内细粒度分支有 Flag 和 Predication 两种实现方式。Flag 方式将条件判断合并为一个表达式，阵列同时计算两种结果，通过 flag 选择输出。这种方式无限额外的硬件分支逻辑，设计复杂度低，但同时计算的分支会导致冗余运算。Predication 方式中 PE 输出一对互补的条件位，硬件根据条件位关断不执行的分支电路。这种方式无冗余计算利用率高，但 PE 需要支持条件位，增加了硬件设计和控制逻辑复杂度。

参考资料

本文由作者按照 CC BY 4.0 进行授权